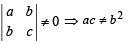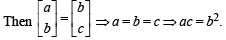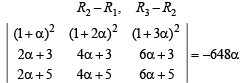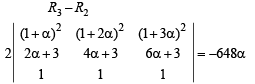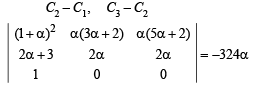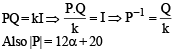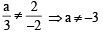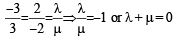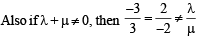Test: MCQs (One or More Correct Option): Matrices and Determinants | JEE Advanced - JEE MCQ
12 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Matrices and Determinants | JEE Advanced
The determinant 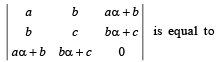 zero, if
zero, if
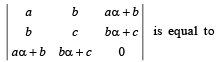 zero, if
zero, if| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let M and N be two 3 × 3 non-singular skew- symmetric matrices such that MN = NM. If PT denotes the transpose of P, then M2N2 (MTN)–1 (MN–1)T is equal to
If the adjoint of a 3 x 3 matrix P is  then the possible value(s) of the determinant of P is (are)
then the possible value(s) of the determinant of P is (are)
For 3 × 3 matrices M and N, which of the following statement(s) is (are) NOT correct?
Let ω be a complex cube root of unity with ω ≠ 1 and P = [pij] be a n × n matrix with pij = ωi+j. Then p2 ≠ 0, when n =
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible if
Let M and N be two 3 × 3 matrices such that MN = NM. Further, if M ≠ N2 and M2 = N4, then
Which of the following values of a satisfy the equation
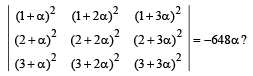
Let X and Y be two arbitrary, 3 × 3, non-zero, skew-symmetric matrices and Z be an arbitrary 3 × 3, non zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric?
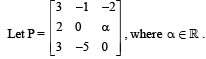 Suppose Q = [qij] is a matrix such that PQ = kI, where
Suppose Q = [qij] is a matrix such that PQ = kI, where 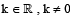 and I is the identity matrix of order 3.
and I is the identity matrix of order 3.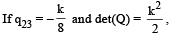 then
then
Let 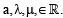 Consider th e system of lin ear equations
Consider th e system of lin ear equations
ax + 2y = λ
3x – 2y = μ
Which of the following statement(s) is (are) correct?
|
347 docs|185 tests
|
|
347 docs|185 tests
|


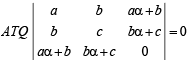
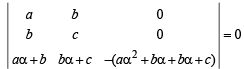
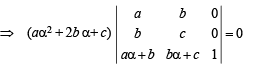
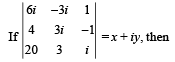
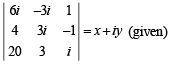
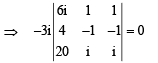
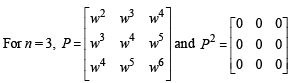
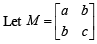 where a, b, c are integers.
where a, b, c are integers.