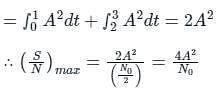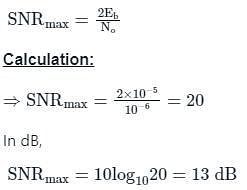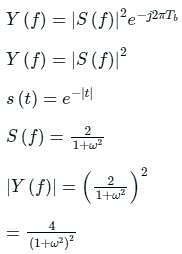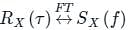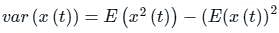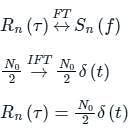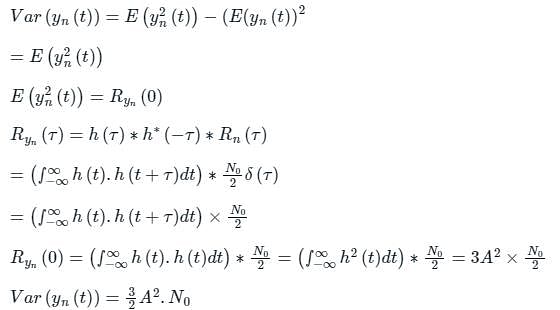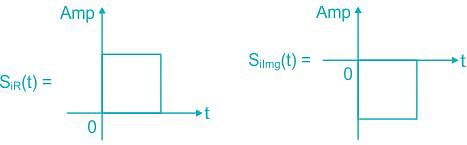Test: Matched Filter - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Communication System - Test: Matched Filter
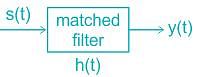
Which of the following statements about the matched filter in a communication receiver are correct ?
(A) It may produce phase error if synchronization is improper
(B) Its impulse response depends on the singal shape
(C) The characteristics of the matched filter is matched with the transmitted data
(D) It produces inter symbol interference
(E) It measures the correlation between incoming received message and its impulse response
Choose the correct answer from the options given below :
(A) It may produce phase error if synchronization is improper
(B) Its impulse response depends on the singal shape
(C) The characteristics of the matched filter is matched with the transmitted data
(D) It produces inter symbol interference
(E) It measures the correlation between incoming received message and its impulse response
Choose the correct answer from the options given below :
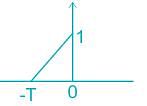
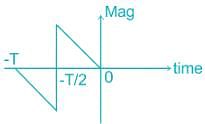
Consider the pulse shape s(t) as shown. The impulse response h(t) of the filter matched to this pulse is

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
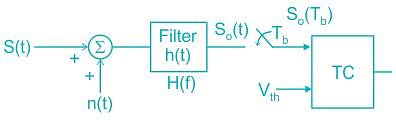
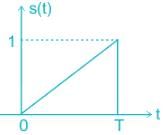
The received signal in a binary communication system is given by r(t) = s(t) + n(t). Where n(t) is AWGN with PSD of N0/2 (W / Hz) and s(t) is shown in the figure below.
The maximum value of signal to noise ratio at the output of the matched filter is _________.

The maximum value of signal to noise ratio at the output of the matched filter is _________.
If Eb, the energy per bit of a binary digital signal, is 10-5 Ws (Watt-Second) and the one-sided power spectral density of the white noise, N0 = 10-6 W/Hz, then the output SNR of the matched filter is
Let  and h(t) is a filter matched to y(t). If y(t) is applied as input to h(t) then the Fourier transform of the output is:
and h(t) is a filter matched to y(t). If y(t) is applied as input to h(t) then the Fourier transform of the output is:
Signal e-|t| is applied to matched filter. The amplitude spectrum of the output signal will be _______.
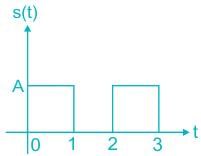
A binary baseband digital communication system employs the signal

for transmission of bits. The graphical representation of the matched filter output y(t) for this signal will be
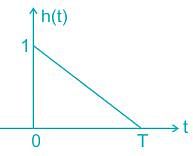
A zero mean white Gaussian noise having power spectral density N0/2 is passed through an LTI filter whose impulse response h(t) is shown in the figure. The variance of the filtered noise at t = 4 is
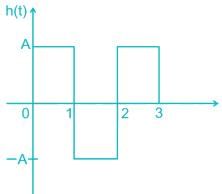
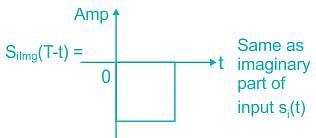
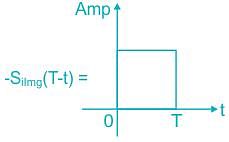
Determine the matched filter response h(t) for signal s(t) shown below:
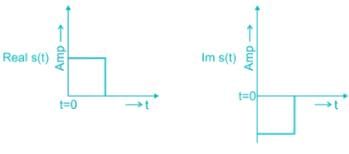
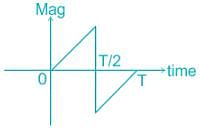
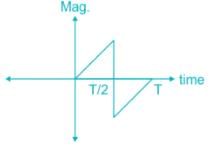
The matched filter response for a given signal, sampled at t = T is:
|
14 videos|38 docs|30 tests
|
|
14 videos|38 docs|30 tests
|