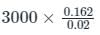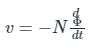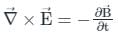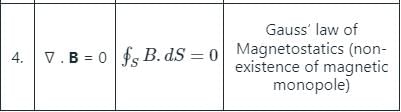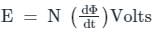Test: Maxwell's Equations Interpretation - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Maxwell's Equations Interpretation
When a conductor connected to an electrical circuit moves in a magnetic field, the direction induced current depends upon
If flux density is represented by 'B' and magnetic field is represented by 'H' in a magnetic circuit, then what will be the energy density in the magnetic field?
What would be the magnitude and direction of average voltage induced across the field coils of a 6-pole DC generator each having 500 turns if there is a magnetic flux of 0.03 Wb/pole when the field is excited and residual magnetism of 0.003 Wb/pole after the field circuit is a is opened in 0.02 second? Consider the field coils to be connected in series.
Following equations are given for retarded time-varying fields
A. ∇2V = -ρ/ε + ω2μεV
B. ∇2V = p/ε + ω2μεV
C. ∇2A = μJ̅ + ω2μεJ̅
D. ∇2A =-μJ̅ + ω2μεA
Choose the correct answer from the options given below:
If the conductor is stationary and the field is changing (varying), then emf induced in it. Such an emf is known as:
Which of the following statements is FALSE for a complex alternating wave which is periodic and have equal positive and negative cycles?
According to Faraday's law, the voltage v induced in the coil with N turns and magnetic flux ϕ is:
Which of the following is NOT a correct Maxwell equation?
The direction of induced e.m.f. can be founded by
Which of the following law states that “whenever the magnetic flux linked with a conductor or coil changes, an emf is induced in it?