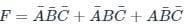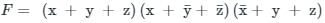Test: POS Form - Electronics and Communication Engineering (ECE) MCQ
7 Questions MCQ Test - Test: POS Form
Given F1 = Π M (0, 4, 5, 6) and F2 = Π M (0, 3, 4, 6, 7). The maxterm expansion for F1F2 is given by:
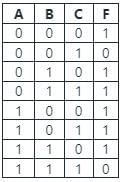
The expression for the truth table given below in POS form is given by:
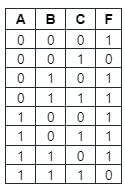

A function F (A, B,C) defined by three Boolean variables A,BC when expressed as sum of products is given by:
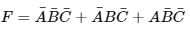
where A̅, B̅ and C̅ are the complements. The POS form of function is
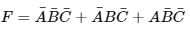
where A̅, B̅ and C̅ are the complements. The POS form of function is
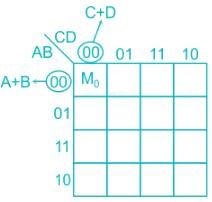
In K-map reduction for 4-variables POS expression, the cell with address 0000 indicates:
A function of Boolean variables x, y and z is expressed in terms of the min-term as F(x,y,z) = Σ(1,2,5,6,7). Which one of the product of sums given below is equal to F(x,y,z)
A function (A, B, C) defined by three boolean variables A, B, and C when expressed as the sum of products is given by:
F = A̅.B̅.C̅ + A̅.B.C̅ + A.B̅.C̅
where, A̅, B̅, and C̅ are the complements of the respective variables. The product of sums (POS) form of the function F is