Test: Perimeters, Areas and Volumes - 2 - UCAT MCQ
10 Questions MCQ Test Quantitative Reasoning for UCAT - Test: Perimeters, Areas and Volumes - 2
Two mutually perpendicular chords AB and CD meet at a point P inside the circle such that AP = 6 cms, PB = 4 units and DP = 3 units. What is the area of the circle?
Cylindrical cans of cricket balls are to be packed in a box. Each can has a radius of 7 cm and height of 30 cm. Dimension of the box is l = 76 cm, b = 46 cm, h = 45 cm. What is the maximum number of cans that can fit in the box?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Figure below shows a box which has to be completely wrapped with paper. However, a single Sheet of paper need to be used without any tearing. The dimension of the required paper could beCAT Mesuration: Cuboid


An inverted right circular cone has a radius of 9 cm. This cone is partly filled with oil which is dipping from a hole in the tip at a rate of 1cm2/hour. Currently the level of oil 3 cm from top and surface area is 36π cm2. How long will it take the cone to be completely empty?
An equilateral triangle ABC is inscribed in a circle with centre O. D is a point on the minor arc BC and ∠CBD = 40º. Find the measure of ∠BCD.
A sphere of radius 12 cm is melted and re-casted into a right circular cone of height 12 cm. The radius of the cone is.
AB is a diameter of a circle with center O. A tangent is drawn at point A. C is a point on the circle such that BC produced meets the tangent at P. If ∠APC = 62º, then find the measure of the minor arc AC(i.e.∠ ABC).
To pack a set of books, Gautam got cartons of a certain height that were 48 inches long and 27 inches wide. If the volume of such a carton was 22.5 cubic feet, what was the height of each carton? [Use 1 foot = 12 inches.]
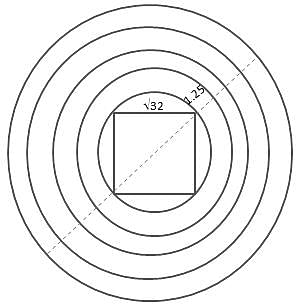
There are 5 concentric circles that are spaced equally from each other by 1.25 cms. The innermost circle has a square of side √(32) cm inscribed in it. If a square needs to be inscribed in the outermost circle, what will be its area?
Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?
|
34 videos|17 docs|16 tests
|
|
34 videos|17 docs|16 tests
|