Test: Propositional Logic - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Propositional Logic
What is logically equivalent to the following statements? "I pass only if you pass" (Note that fail is equivalent to not pass.)
P: The population of Hyderabad is more than Delhi.
Q: Last year, the number of months with 31 days are 7.
choose the correct option based on the truth value of the statements?
Q: Last year, the number of months with 31 days are 7.
choose the correct option based on the truth value of the statements?
Which of the following is correct?
F1 : (p ↔ q)∧(¬ p ↔ q)
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)
F1 : (p ↔ q)∧(¬ p ↔ q)
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)
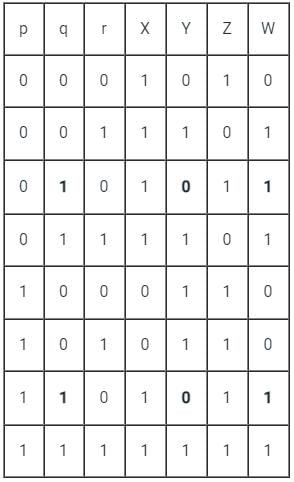
Let p, q, r, s represents the following propositions.
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
The integer x ≥ 2 which satisfies ¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) is __________
Consider the following two statements.
S1: If a candidate is known to be corrupt, then he will not be elected
S2: If a candidate is kind, he will be elected
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
Let p, q, and r be propositions and the expression (p → q) → r be a contradiction. Then the expression (r → p) → q is
“If X, then Y unless Z” is represented by which of the following formulae in propositional logic?
(“¬” is negation “^” is conjunction, and “→” is implication)
Consider the following logical inferences.
I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.
I2: If it rains then the cricket match will not be played.
It did not rain
Inference: The cricket match was played.
Which of the following is TRUE?
p is the proposition “ Indian army moves back”
q is the proposition “ Chinese army moves back”
r is the proposition “ There is no war”
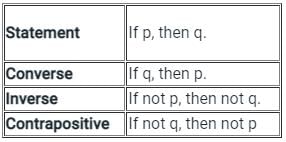
Then what is the contrapositive of the statement “ If Indian army moves back and Chinese army moves back, then there is no war”
If p = a number from {8, 9, 10, 11, 12}
q = not a composite number
r = a square number
s = a prime number
then what is the value of ~((p → ~q)∧(~r ∨~S) )