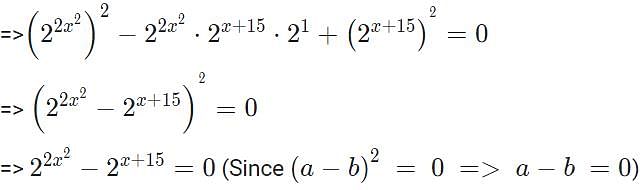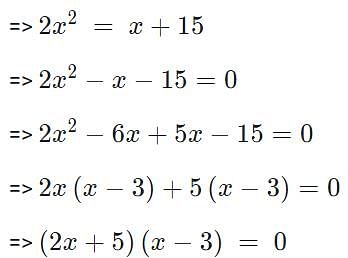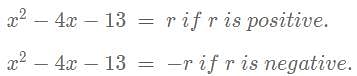Test: Quadratic Equations- 1 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Quadratic Equations- 1
Suppose one of the roots of the equation ax2 - bx + c = 0 is 2+ √3, Where a,b and c are rational numbers and a ≠ 0. If b = c3 then |a| equals.
If the roots x1 and x2 are the roots of the quadratic equation x2 - 2x + c = 0 also satisfy the equation 7x2 - 4x1 = 47, then which of the following is true?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let p and q be the roots of the quadratic equation x2 - (α - 2)x - α - 1 = 0. What is the minimum possible value of p2 + q2?
A quadratic function f(x) attains a maximum of 3 at x = 1. The value of the function at x = 0 is 1. What is the value of f (x) at x = 10?
Suppose k is any integer such that the equation 2x2 + kx + 5 = 0 has no real roots and the equation x2 + (k - 5)x + 1 = 0 has two distinct real roots for x. Then, the number of possible values of k is
If (3 + 2√2) is a root of the equation ax2 + bx + c = 0 and 2√3 is a root of the equation ay2 + my + n = 0 where a, b, c, m and n are integers, then the value of (b/m + c-2b/n) is
The sum of all possible values of x satisfying the equation 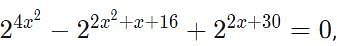 is
is
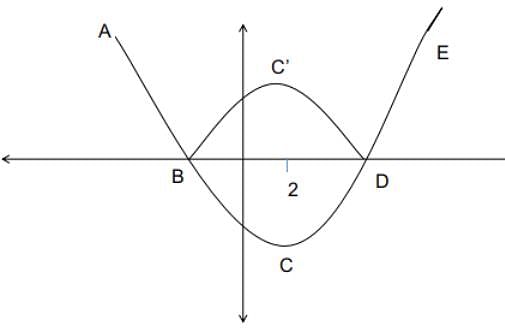
If r is a constant such that ∣x2 − 4x − 13∣ = r has exactly three distinct real roots, then the value of r is
The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 + c?
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|


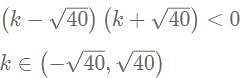

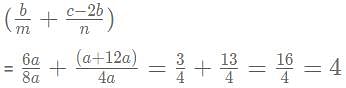
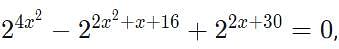 which can be written as:
which can be written as: