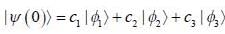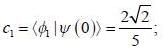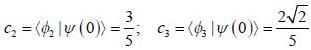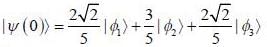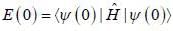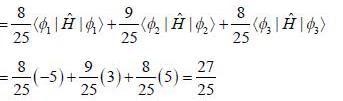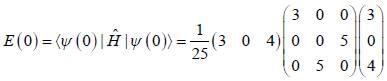Test: Quantum Mechanics - 1 - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2025 - Test: Quantum Mechanics - 1
Consider a two state system with normalized energy eigen state ψ1 & ψ2 and energy E1 < E2 what is the possible range for the expectation value of  on an orbitrary linear combination of two state
on an orbitrary linear combination of two state
 on an orbitrary linear combination of two state
on an orbitrary linear combination of two stateSuppose a wave function 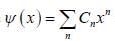 and an operator is given by
and an operator is given by 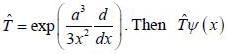 is given by
is given by
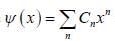 and an operator is given by
and an operator is given by 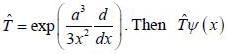 is given by
is given byConsider the following Stem-Gerlach apparatus incoming beam consist of electron 2/3 of them having spin 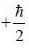 and other 1/3 have spin
and other 1/3 have spin 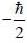 in the z-direction
in the z-direction
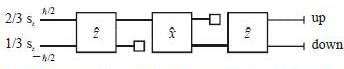
what fraction of the incident beam are detected in the up and down outputs of the apparatus
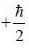 and other 1/3 have spin
and other 1/3 have spin 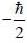 in the z-direction
in the z-direction
what fraction of the incident beam are detected in the up and down outputs of the apparatus
Consider a system whose initial state at r = 0 is given in term of a complete and orthonormal set of three vectors 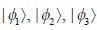 as follows
as follows 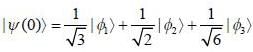 the probability of find tlie system at tune t in state
the probability of find tlie system at tune t in state 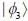 is _______ (upto two decunalplaces)
is _______ (upto two decunalplaces)
An election is confined in an infinite square well of width 10x10^-15 m. Calculate the wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).
Consider a tliree dimensional harmonic oscillator with Hamiltonian
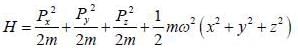
The number of distinct eigenstates with energy eigenvalue 5/2 ℏω is_________
(Answer should be an integer).
Consider an operator 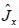 for a system of total angular momentum j = 1 then winch of the following state having non zero uncertainty
for a system of total angular momentum j = 1 then winch of the following state having non zero uncertainty
In the simple harmonic oscillator
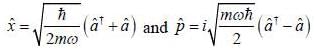
what are the condition on m and m' for 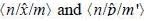 to be non-zero
to be non-zero
Find the differential cross-section for die scattering of slow (low velocity) particle from a spherical delta poten- tial V (r) = V0 δ (r - a)
For case of n = 2, ℓ = 1, m = 0 the value of r at which the radial probability density of the hydrogen atom reaches its maximum is ____ a0. 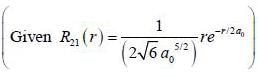 (answer should be an integer)
(answer should be an integer)
Consider a system winch is mtially in the state 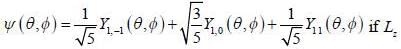 was measured with value -ℏ, the probability is_______(upto one decimal place)
was measured with value -ℏ, the probability is_______(upto one decimal place)
An electron is confined in the ground state of a one dimensional harmonic oscillator such that 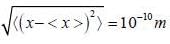 energy required to excite to its first excited state is _____ (MeV)
energy required to excite to its first excited state is _____ (MeV)
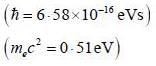
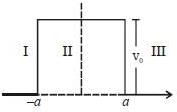
A particle of mass m coming in from the left with energy E > 0, encounters barrier potential
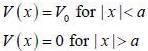
The wave function is given by
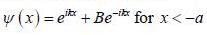
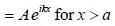
The constant A and B satisfy which one of the following relation?
Calculate the width of the probability density distribution for r(i.e Br) for hydrogen atom for the state 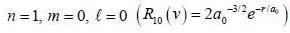
At t = o, a state is given by
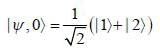
Where 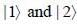 are ortlionomial stationary states of energy El & E2 respectively with E2 > El what is the shortest tune T > 0 for w hich
are ortlionomial stationary states of energy El & E2 respectively with E2 > El what is the shortest tune T > 0 for w hich 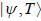 is orthogonal to
is orthogonal to 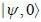
If the state of a particle moving in one dimensional harmonic oscillator is given by
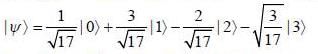
Where 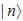 represent the normalized nth energy eigenstate find the expectation value of number operator
represent the normalized nth energy eigenstate find the expectation value of number operator 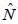 ( n = 0,1,2,3....)
( n = 0,1,2,3....)
A particle of mass m moves in a one dimensional potential box
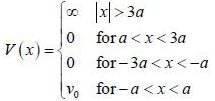
Consider the V0 part as perturbation, using first order perturbation method calculate the energy of ground state.
A spin state precesses in a magnetic field same way as the classical magnetic dipole precesses in magnetic field with lasmor frequency given by 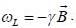 consider the Hamiltonian
consider the Hamiltonian 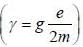
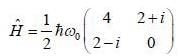 Larrnor frequency
Larrnor frequency 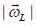 is (in tem is of ω0)
is (in tem is of ω0)
(answer should b e an mteger)
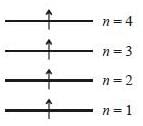
Consider a system of four non-interacting identical spin 1/2 particles that are in same state 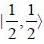 and confined to move in a one-diniension infinite potential well of length a: V(x) = 0 for 0 < x < a and V(x) = ∞ forotlier values of x. The ground state energy of the system in units of
and confined to move in a one-diniension infinite potential well of length a: V(x) = 0 for 0 < x < a and V(x) = ∞ forotlier values of x. The ground state energy of the system in units of 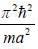 is (answer should be an integers).
is (answer should be an integers).
Consider a system whose intial state 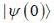 and hamiltonian are given by
and hamiltonian are given by
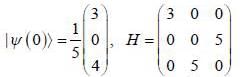
find the total energy of a system
|
1 docs|34 tests
|


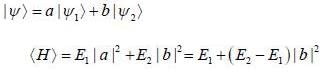
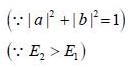
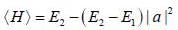
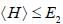 ......(2)
......(2)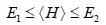
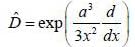
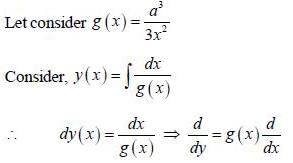
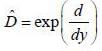
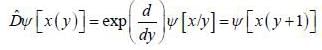
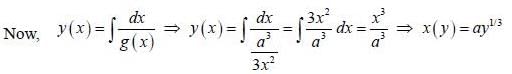
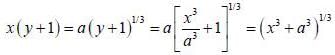
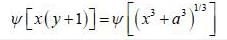


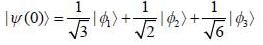
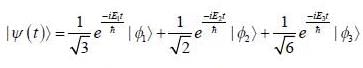
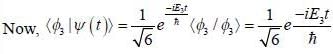
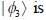
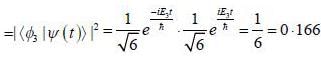
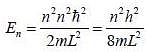
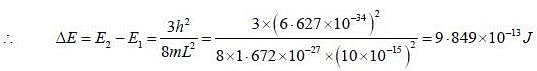
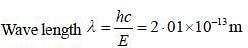
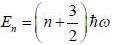
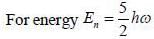
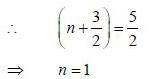
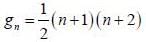
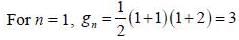
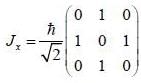
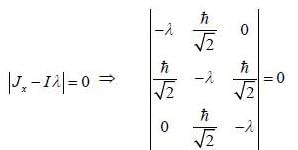
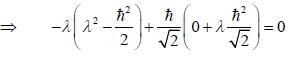
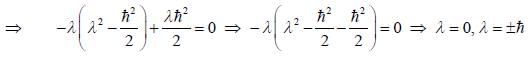
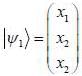 is the eigen function of Jx corresponding the eigen value λ = 0
is the eigen function of Jx corresponding the eigen value λ = 0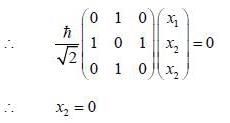
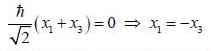
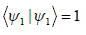
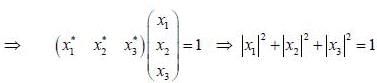
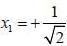
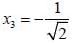
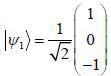
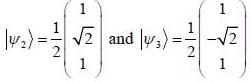
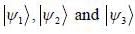 are the eigen state of operator Jx.
are the eigen state of operator Jx.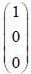 is not an eigen states of Jx.
is not an eigen states of Jx.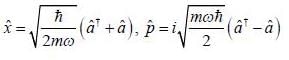
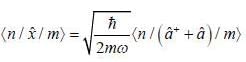
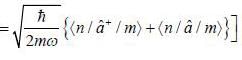
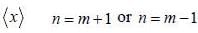
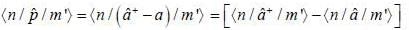
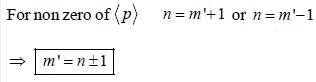
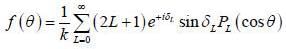
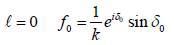
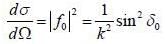
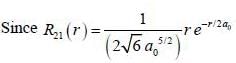
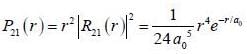
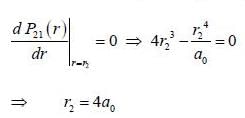
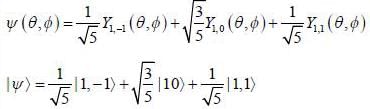
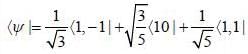
 probability of measuring Lz in
probability of measuring Lz in 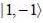 state is
state is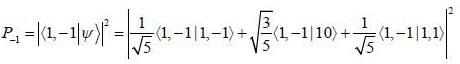
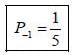
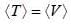
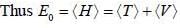
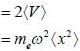
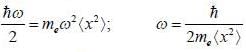
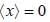
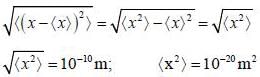
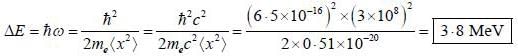
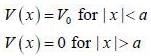
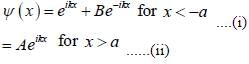

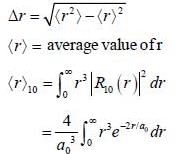

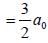
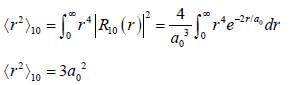
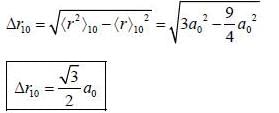
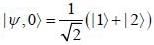
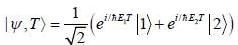
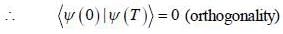
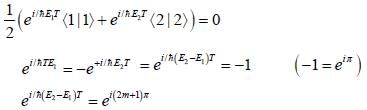
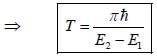
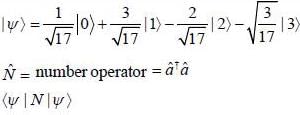
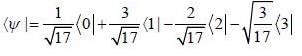
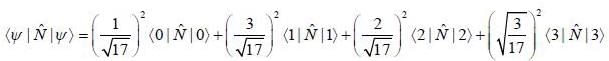
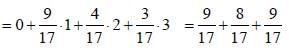
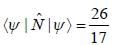
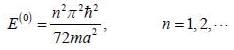
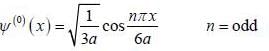
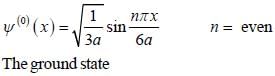
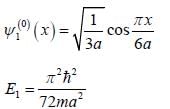
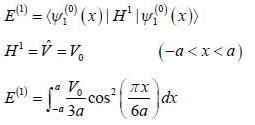
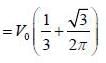
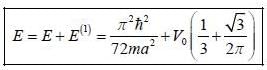
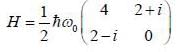
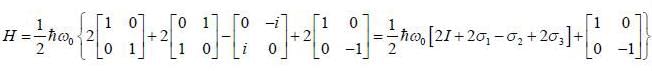
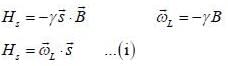
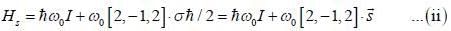
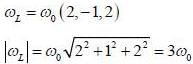

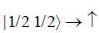
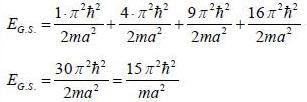
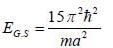
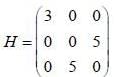
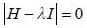
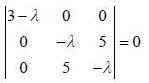
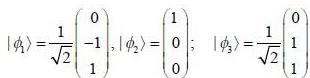
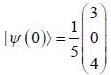
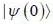 in terms of eigenvectors.
in terms of eigenvectors.