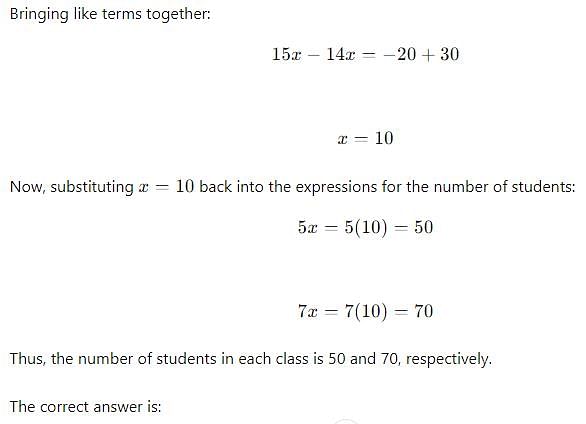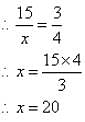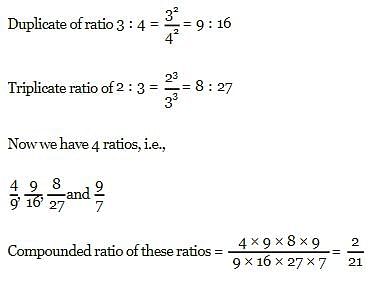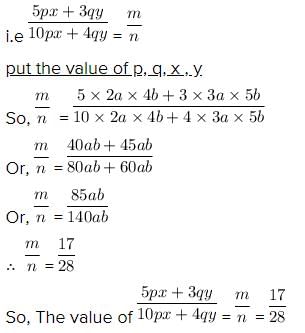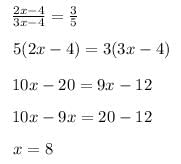Test: Ratio And Proportion, Indices, Logarithms - 3 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Ratio And Proportion, Indices, Logarithms - 3
If 2x x 3y x 5z = 360 then what is the value of x, y, z?
Find the value of [log10 25 - log10(23) + log10(4)2]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If 2x-2x-1=4 then xx is equal to :
What must be added to each term of the ratio 49:68, so that it becomes 3:4?
If A, B and C started a business by investing Rs. 1,26,000, Rs. 84,000 and Rs. 2,10,000. If at the end of the year profit is Rs. 2,42,000 then the share of each is:
If a: b = 2 : 3, b: c = 4: 5, and c : d = 6: 7, then find the value of a: b : c : d
Log4 (x2+x) - log4 (x+1) = 2. Find x
Fourth proportional to x, 2x, (x+1) is:
If x=31/3+3-1/3 then find value of 3x3-9x
The value of log2 (log5 625) is :
If A:B=2:5, then (10A+3B):(5A+2B) is equal to
Find the sub-duplicate ratio of 81 : 64 ?
The sub duplicate ratio of 25:36 is
The ratio compounded of 2:3, 9:4, 5:6 and 8:10 is
The sub triplicate ratio of 8:27 is
The triplicate ratio of 2:3 is
The student of two classes are in the ratio 5:7, if 10 students left from each class, the remaining students are in the ratio of 4:6 then the number of students in each class is:
The ratio of two quantities is 3:4. If the antecedent is 15, the consequent is
The ratio compounded of 4:9, the duplicate ratio of 3:4, the triplicate ratio of 2:3 and 9:7is
The duplicate ratio of 3:4 is
The ratio compounded of 4:9 and the duplicate ratio of 3:4 is
The recurring decimal 2.7777………….can be expressed as
The ratio of the quantities is 5:7. If the consequent of its inverse ratio is 5, the antecedent is
The angles of a triangle are in ratio 2:7:11. The angles are
If p:q =2:3 and x:y = 4:5, then the value of 5px + 3qy: 10px + 4qy is
Two numbers are in the ratio 2:3. If 4 be subtracted from each, they are in the ratio 3:5. The numbers are
If x:y = 3:4, the value of (x2y+xy2):(x3 +y3) is
P, Q and R are three cities. The ratio of average temperature between P and Q is 11:12 and that between P and R is 9:8. The ratio between the average temperature of Q and R is
The ratio of two numbers is 7:10 and their difference is 105. The numbers are
|
115 videos|174 docs|98 tests
|
|
115 videos|174 docs|98 tests
|


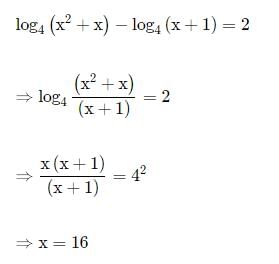

 a∶b
a∶b