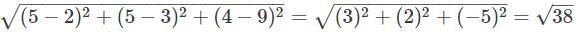Test: Section Formula - SAT MCQ
10 Questions MCQ Test - Test: Section Formula
The coordinates of a point dividing the line segment joining (1, 2, 3) and (4, 5, 6) internally in the ratio 2:1 is _______.
The coordinates of a point dividing the line segment joining (1, 2, 3) and (4, 5, 6) externally in the ratio 2:1 is __________.
The ratio in which line joining (1, 2, 3) and (4, 5, 6) divide X-Y plane is ________
Find the points which trisects the line joining (4, 9, 8) and (13, 27, -4).
If P (2, 3, 9), Q (2, 5, 5) and R (8, 5, 3) are vertices of a triangle then find the length of median through Q.
In which ratio (3, 4, 5) divides the line segment joining (1, 2, 3) and (4, 5, 6) internally?
If coordinates of vertices of a triangle are (7, 6, 4), (5, 4, 6), (9, 5, 8), find the coordinates of centroid of the triangle.
Find the points which trisects the line joining (4, 9, 8) and (13, 27, -4).
If P (2, 3, 9), Q (2, 5, 5) and R (8, 5, 3) are vertices of a triangle then find the length of median through P.


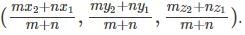
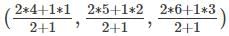
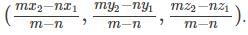
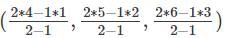 = (7, 8, 9).
= (7, 8, 9).
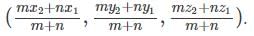
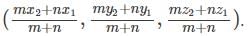
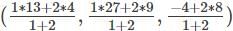 = (7, 15, 4)
= (7, 15, 4)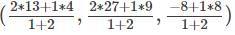 = (10, 21, 0)
= (10, 21, 0)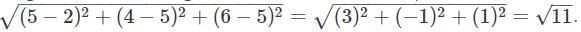
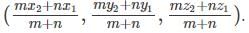
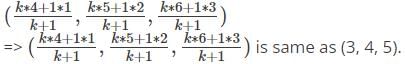
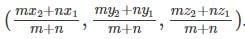
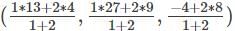 = (7, 15, 4)
= (7, 15, 4) = (10, 21, 0)
= (10, 21, 0)