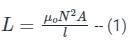Test: Self Inductance - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test Electromagnetic Fields Theory (EMFT) - Test: Self Inductance - 1
When the current changes from +2A to -2A in 0.05 second, an emf of 8V is induced in the coil. The coefficient of self inductance of the coil is
An emf of 5 V is produced by self - inductance, when the current changes at a steady rate from 3 A to 2 A in 1 ms. The value of self - inductance is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If we apply law of conversion of energy to electromagnetic induction, electrical energy induced in a conductor comes from
When number of turns per unit length of a solenoid is doubled, its self inductance becomes:
When the length of the solenoid is doubled without any change in the number of turns and the area of the coil.Then its self-inductance will
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance:
If we increase the current in an inductor, self inductance of the inductor will __________.
The coefficient of self-inductance of a solenoid is 0.18 mH. If a core of soft iron of relative permeability 900 is inserted, then the coefficient of self-inductance will become nearly
If the magnitude of the applied potential is decreased in the coil, then the direction of the induced current and the current due to applied potential will be
|
10 videos|45 docs|56 tests
|
|
10 videos|45 docs|56 tests
|