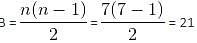Test: Sorting - 2 - CUET Humanities MCQ
10 Questions MCQ Test Computer Science Practice Tests: CUET Preparation - Test: Sorting - 2
Consider an array of 5 elements - 47, 25, 82, 16 and 31. How many times will the numbers be swapped according to quick sort algorithm to sort them in ascending order?
What is the output of the first step of selection sort performed on the following input?
64 25 12 22 11
Consider the following array:
{16, 4, 9, 3, 18, 14, 15}
For the array, if A is the number of comparisons in bubble sort and B is the number of comparisons in selection sort, then
How many comparisons are needed to sort an array of length 5 if a straight selection sort is used and the array is already in the opposite order?
You have to sort a list L, consisting of a sorted list followed by a few 'random' elements. Which of the following sorting method would be most suitable for such a task?