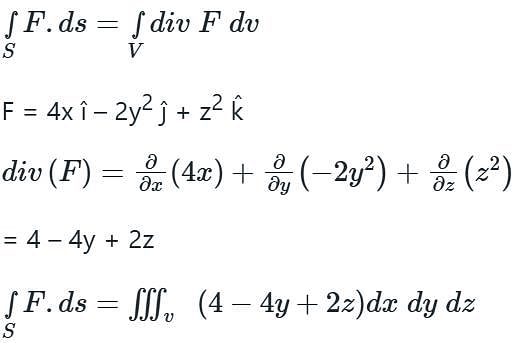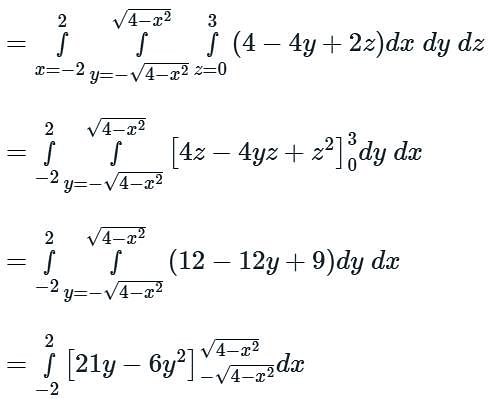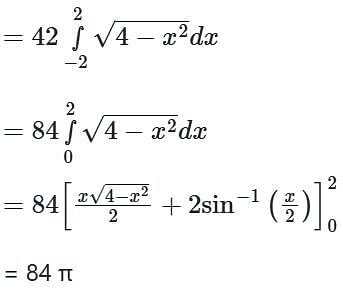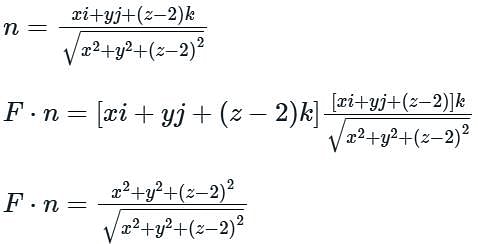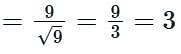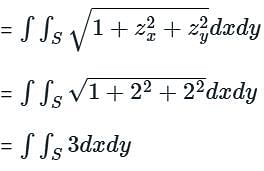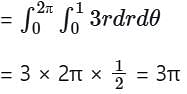Test: Surface Integral - Electrical Engineering (EE) MCQ
10 Questions MCQ Test Electromagnetic Fields Theory (EMFT) - Test: Surface Integral
Gauss law for electric field uses surface integral. State True/False
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Coulomb’s law can be derived from Gauss law. State True/ False
Compute the Gauss law for D= 10ρ3/4 i, in cylindrical coordinates with ρ= 4m, z=0 and z=5.
Find the value of divergence theorem for A = xy2 i + y3 j + y2z k for a cuboid given by 0<x<1, 0<y<1 and 0<z<1.
The ultimate result of the divergence theorem evaluates which one of the following?
If D = 2xy i + 3yz j + 4xz k, how much flux passes through x = 3 plane for which -1<y<2 and 0<z<4?
Evaluate 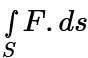 where F = 4x î – 2y2 ĵ + z2 k̂ and S is the surface bounding the region x2 + y2 = 4, z = 0 and z = 3.
where F = 4x î – 2y2 ĵ + z2 k̂ and S is the surface bounding the region x2 + y2 = 4, z = 0 and z = 3.
Consider the hemisphere x2 + y2 + (z - 2)2 = 9, 2 ≤ z ≤ 5 and the vector field F = xi + yj + (z - 2)k The surface integral ∬ (F ⋅ n) dS, evaluated over the hemisphere with n denoting the unit outward normal vector, is
Let S be the portion of the plane z = 2x + 2y − 100 which lies inside the cylinder x2 + y2 = 1. If the surface area of S is απ, then the value of α is equal to ___________.
|
10 videos|45 docs|56 tests
|
|
10 videos|45 docs|56 tests
|