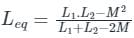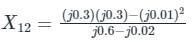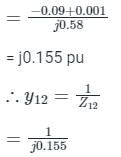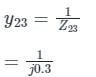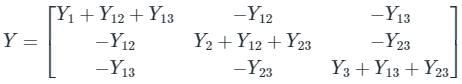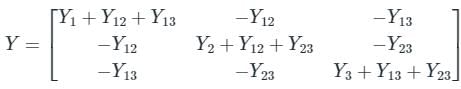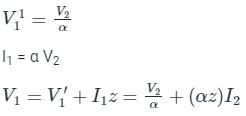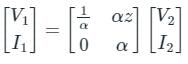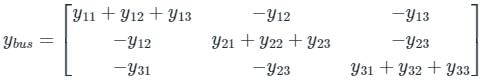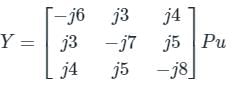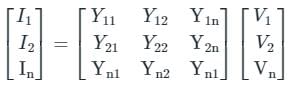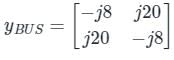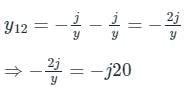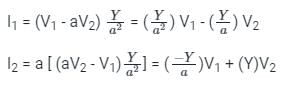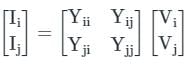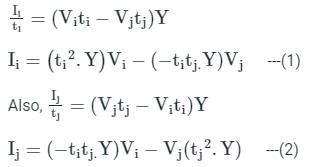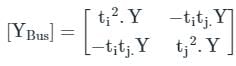Test: Y Bus Matrix - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Y Bus Matrix
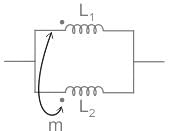
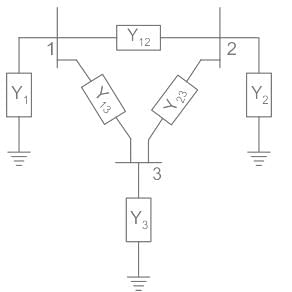
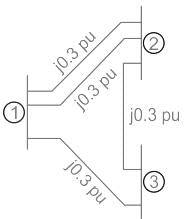
The 3-bus system is shown in the figure, Two lines are connected between bus 1 and bus 2 is having a mutual effect of M = j0.01(additive). Find the Y22 element of the YBus matrix of the system.

Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known as
For formation of the Y bus matrix (using node voltage analysis) in power system network modelling ______ is used
A 1000 × 1000 bus admittance matrix for an electric power system has 8000 non-zero elements. The minimum number of branches (transmission lines and transformers) in this system are _____ (up to 2 decimal places).
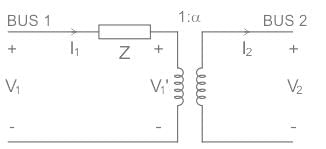
The figure shows the per-phase representation of a phase-shifting transformer connected between buses 1 and 2, where α is a complex number with non-zero real and imaginary parts.
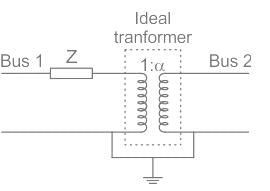
For the given circuit Ybus and Zbus are bus admittance matrix and bus impedance matrix respectively, each of size 2 × 2. Which one of the following statements is true?
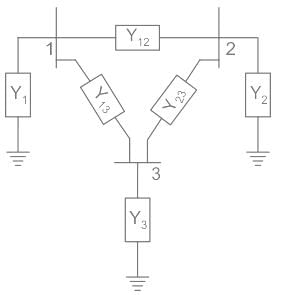
A 3 – bus power system network consists of 3 transmission lines. The bus admittance matrix of the uncompensated system is
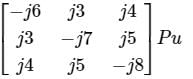
If the shunt capacitance of all transmission lines is 50% compensated, the imaginary part of the 3rd row 3rd column element (in pu) of the bus admittance matrix after compensation is
In an n-bus power system, considering n-nodes network, the size of ybus is
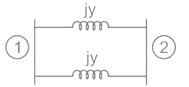
The Ybus matrix of a two-bus power system having two identical parallel lines connected between them in pu is given as 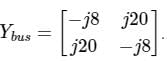
The magnitude of the series reactance of each line in pu (round off up to one decimal place) is ____________.
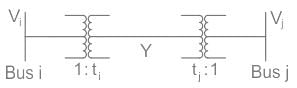
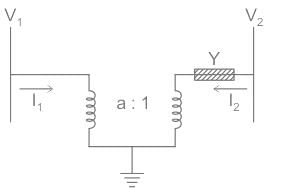
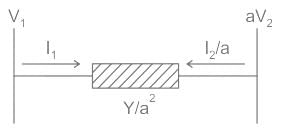
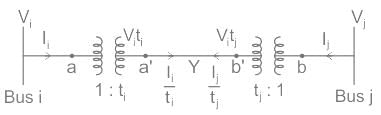
Two buses, i and j, are connected with a transmission line of admittance Y, at the two ends of which there are ideal transformers with turns ratios as shown. Bus admittance matrix for the system is: