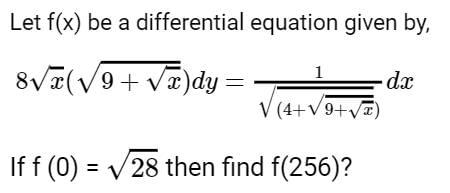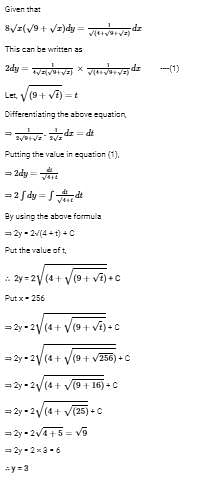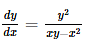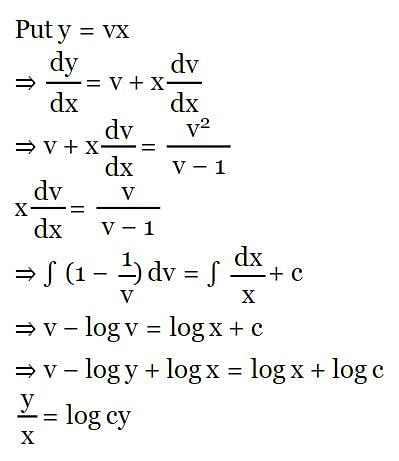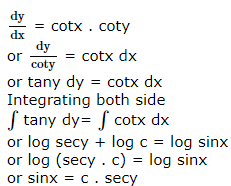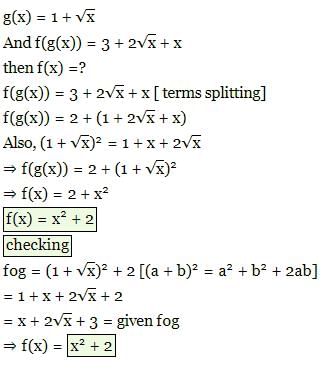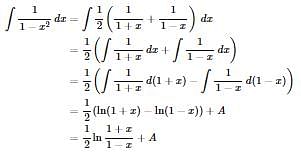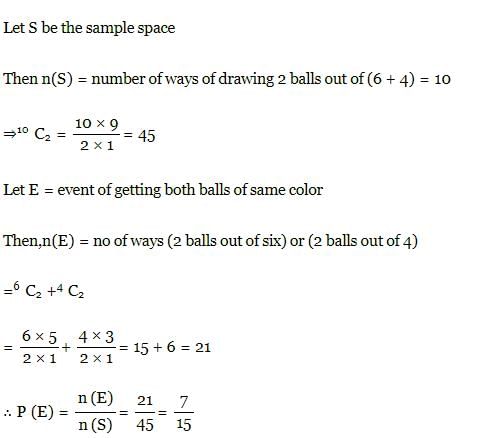VITEEE Maths Test - 1 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE Maths Test - 1
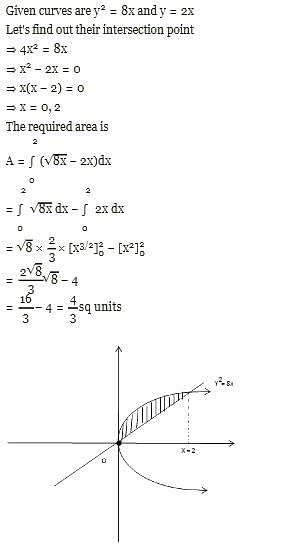
The area enclosed by the parabola y2 = 8x and the line y = 2x is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Locus of a point P equidistant from two fixed points A and B is ____________
A card is drawn and replaced in an ordinary pack of playing cards. The number of times a card must be drawn so that the probability of getting atleast a club card is greater than 3/4 is
The family of curves, in which the subtangent at any point to any curve is double the abscissa, is given by
The differential of sin-1[(1-x)/(1+x)] w.r.t. √x is equal to
Suppose that g(x) = 1 + √x and f(g(x)) = 3 + 2√x + x, then f(x) is
If sin-1x + sin-1y = 2π/3, then cos-1 x + cos-1 y is equal to
q : A man is rich
Then , the statement , ' if a man is not happy , then he is not rich ' is written as
If B is a non-singular matrix and A is a square matrix, then det (B-1AB) =
If the probability that A and B will die within a year are p and q respectively, then the probability that only one of them will be alive at the end of the year, is
We have (n+1) white balls and (n+1) black balls. In each set the balls are numbered from 1 to (n+1). If these balls are to be arranged in a row so that two consecutive balls are of different colours, then the number of these arrangements is
A bag contains 6 white and 4 black balls. Two balls are drawn at random. The probability that they are of the same colour is
A fair dice is tossed repeatedly until six shows up 3 times. The probability that exactly 5 tosses are needed is
A rope of length 5 metres is tightly tied with one end at the top of a vertical pole and other end to the horizontal ground. If the rope makes an angle 30ο to the horizontal, then the height of the pole is
Let the harmonic means and the geometric mean of two positive numbers be in the ratio 4 : 5. The two numbers are in the ratio
Which one of the following is a source of data for primary investigations?
|
1 videos|2 docs|73 tests
|
|
1 videos|2 docs|73 tests
|