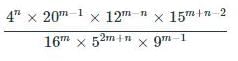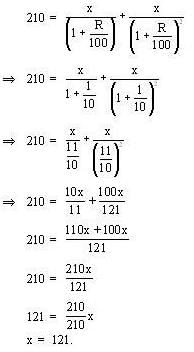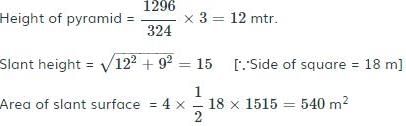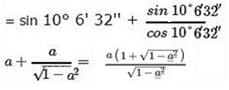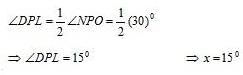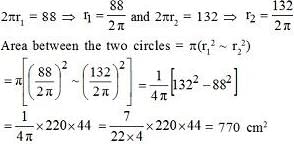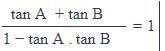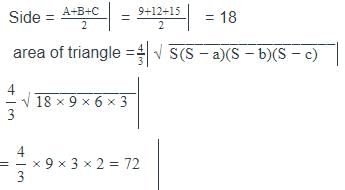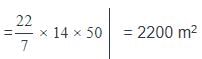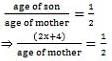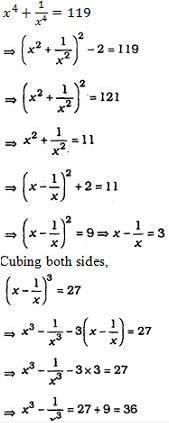RRB JE ECE (CBT I) Mock Test- 1 - Electronics and Communication Engineering (ECE) MCQ
30 Questions MCQ Test - RRB JE ECE (CBT I) Mock Test- 1
Perimeter of an equilateral triangle is equal to the circumference of a circle. The ratio of their areas is :
(Use π= 22/7)
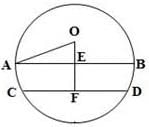
AB = 8 cm and CD = 6 cm are parallel chords on the same side of the centre of a circle. The distance between them is 1cm. The radius of the circle is:
A tank that would normally be filled in 8 hours is now taking 2 hours more because of a leak. In how much time will the leak empty the full tank?
A sum of Rs. 210 was taken as a loan. This is to be paid back in two equal installments. If the rate of interest be 10% compounded annually, then the value of each installment is
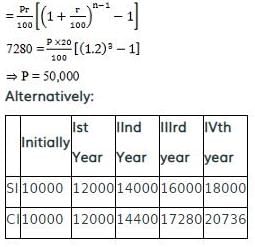
The difference between simple and compound interest for the fourth year is ₹ 7280 at 20% p.a. What is the sum?
At present, the sum of ages of R and K is 63 years. The ratio of their ages after 7 years will be 7:4; what is the present age of R?
If cosec θ = x + 1/4x, then the value of cosec θ + cot θ is:
Base of a right pyramid is a square of area 324 sqm. If the volume of the pyramid is 1296 cu.m., then the area (in m2) of the slant surface is:
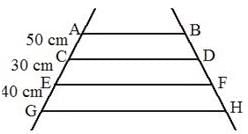
In the given figure AB || CD || EF || GH and BH = 100 cm. Find the value of DF.
If sin (10° 6’ 32”) = a, then the value of cos (79° 53’ 28”) + tan (10° 6’ 32”) is:
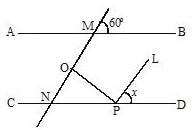
In the figure AB || CD, ∠DPL= 1/2∠NPO, OP is the perpendicular on MN, the value of xº is:
Find the area between two concentric circles of circumference 88 cm and 132 cm.
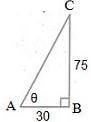
A man moving at a speed of 36 kmph covered the shadow of a tower of height 75 m in 3 seconds. If the height of the person is 1.75 m, the length of the shadow cast by the man in meters is:
A dress is 25% off. If both the cost and selling prices are ₹ 100 less, the profit would be 35%. Find its cost price?
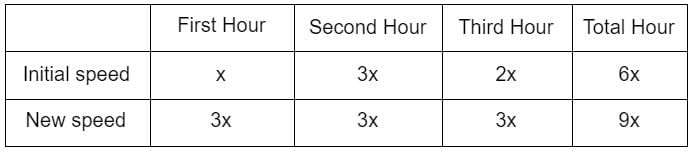
The speed of a car during the second hour of its journey is thrice that in the first hour. Also, its third-hour speed is the average speed of the first two hours. Had the car travelled at the second hour’s speed during all the first three hours, then it would have travelled 150 km more. Find the percentage reduction in time if the original distance covered by the second hour’s speed:
If A+B = 45°, then find the value of tan A + tan B + tan A tan B.
If a + b +c = 13, what is the maximum value of (a -3)(b -2) (c + 1) ?
The length of three medians of a triangle are 9 cm, 12 cm and 15 cm. The area (in sq. cm) of the triangle is:
The floor of a room is of size 4 m x 3 m, and its height is 3 m. The walls and ceiling of the room require painting. The area to be painted is
If 5 girls can embroider a dress in 9 days, then the number of days taken by 3 girls will be _____.
How many metres length of cloth 10 m wide will be required to make a conical tent with base radius of 14 m and height is 48 m?
Two trains are travelling in the same direction at 40 kmph, and 22 kmph completely pass off another in 1 minute. If the length of the first train is 125 metres, what is the length of the second train?
The ratio between the ages of a father and a son at present is 5: 2, respectively. Four years hence the ratio between the ages of the son and his mother will be 1: 2 respectively. What is the ratio between the present ages of the father and the mother, respectively?
If x4 + 1/x4 =119 and x > 1, then the value of x3 − 1/x3 is:
The total annual Co2 emissions from various sectors are 5 MMT. In the pie chart given below, the percentage distribution to Co2 emission from various sectors are indicated.
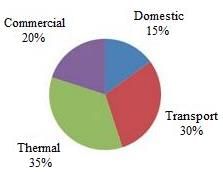
Q. Emission of Domestic sector is how much % of transport and commercial sector combined?
The total annual Co2 emissions from various sectors are 5 MMT. In the pie chart given below, the percentage distribution to Co2 emission from various sectors are indicated.
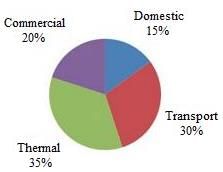
Q. Which of the following sectors have an emission difference of 1 MMT between them?
Twenty percent of Anuj’s annual salary is equal to seventy-five per cent of Raj’s annual salary. Raj’s monthly salary is 60% of Ravi’s monthly salary. If Ravi’s annual salary is Rs. 1.44 lacs, what is Anuj’s monthly salary?
The product of two successive numbers is 4032. Which is the greater of the two numbers?