Test: Graphs & Hashing- 2 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Graphs & Hashing- 2
The average search time of hashing, with linear probing will be less if the load factor
A hash table can store a maximum of 10 records. Currently there are records in locations 1, 3, 4, 7, 8, 9, 10. The probability of a new record going into location 2, with a has function resolving collisions by linear probing is
Consider a hashing function that resolves collision by quadratic probing. Assume the address space is indexed from 1 to 8. Which of the following locations will never be probed if a collision occurs at position 4?
A has table has space for 100 records. What is the probability of collision before the table is 10% full?
A hash function randomly distributes records one by one in a space that can hold x number of records. The probability that the mth record is the first record to result in collision is
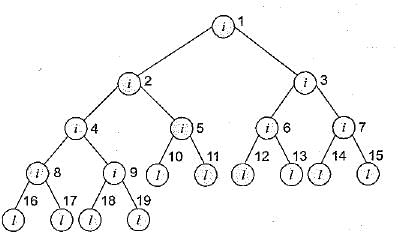
In the given binary tree, using array (the array starts from index 1), you can store the node 4 at location,
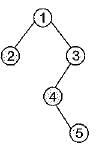
A binary tree in which every non-leaf node has non-empty left and right subtrees is called a strictly binary tree. Such a tree with 10 leaf nodes
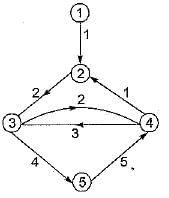
The center of the graph in above questions is the node labeled
In which of the following cases, linked list implementations of sparse matrices consumes the same memory space as the conventional way of storing the entire array?
(Assume all data-types need the same amount of storage.)
|
55 docs|215 tests
|
|
55 docs|215 tests
|