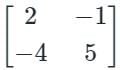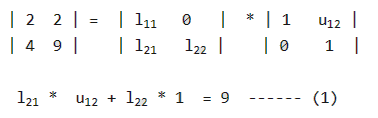Test: Linear Algebra- 2 - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Linear Algebra- 2
The rank of a 3 x 3 matrix C (= AB), found by multiplying a non-zero column matrix A of size 3 x 1 and a non-zero row matrix B of size 1 x 3, is
In questions 1.1 to 1.7 below, one or more of the alternatives are correct. Write the code letter(s) a, b, c, d corresponding to the correct alternative(s) in the answer book. Marks will be given only if all the correct alternatives have been selected and no incorrect alternative is picked up. 1.1). The eigen vector (s) of the matrix
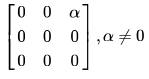
is (are)
Consider the following matrix
If the eigenvalues of A are 4 and 8, then
Consider the following determinant
Which of the following is a factor of Δ?
Let A be a matrix such that Ak = 0. What is the inverse of I - A?
F is an n*n real matrix. b is an n*1 real vector. Suppose there are two n*1 vectors, u and v such that, u ≠ v and Fu = b, Fv = b. Which one of the following statements is false?
Perform the following operations on the matrix
i. Add the third row to the second row
ii. Subtract the third column from the first column.
The determinant of the resultant matrix is _____.
In the LU decomposition of the matrix , if the diagonal elements of U are both 1, then the lower diagonal entry of
of L is_________________.
Let the characteristic equation of matrix M be λ2 - λ - 1 = 0 . Then
Consider the following statements:
• SI: The sum of two singularn n x n matrices may be non-singular
• S2: The sum of two n x n non-singular matrices may be singular
Which one of the following statements is correct?
How many 4 x 4 matrices with entries from have odd determinant?
Hint: Use modulo arithmetic.
Let A be an n × n matrix of the following form.
What is the value of the determinant of A?
If matrix 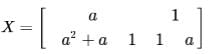 and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is
and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is
The number of different symmetric matrices with each element being either 0 or 1 is: (Note: (2,X) is same as 2X)
The rank of the following matrix, where is a real number is
Let A and B be real symmetric matrices of size. Then which one of the following is true?
Let A, B, C,D be n * n matrices, each with non-zero determinant. If ABCD = I, then B-1 is
In an M × N matrix all non-zero entries are covered in rows and columns. Then the maximum number of non-zero entries, such that no two are on the same row or column, is
If M is a square matrix with a zero determinant, which of the following assertion (s) is (are) correct?
S1: Each row of M can be represented as a linear combination of the other rows
S2: Each column of M can be represented as a linear combination of the other columns
S3: MX = 0 has a nontrivial solution
S4: M has an inverse
Consider the following system of linear equations
Notice that the second and the third columns of the coefficient matrix are linearly dependent. For how many values of , does this system of equations have infinitely many solutions?
Consider the following system of linear equations :
The system of equations has
How many solutions does the following system of linear equations have?
Consider the following set of equations x + 2y = 54 x+8y = 123x + 6y+3z = 15. This set
|
55 docs|215 tests
|
|
55 docs|215 tests
|