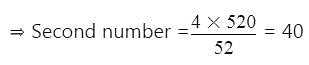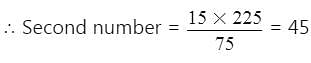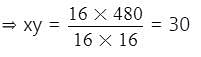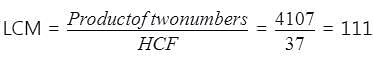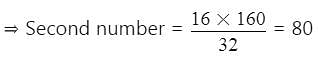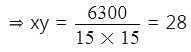MCQ: HCF & LCM - 2 - SSC CGL MCQ
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ: HCF & LCM - 2
The product of two numbers is 2028 and their HCF is 13. The number of such pairs is
LCM of two numbers is 2079 and their HCF is 27. If one of the number is 189, the other number is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The LCM of two numbers is 520 and their HCF is 4. If one of the number is 52, then the other number is
The H.C.F and L.C.M of two numbers are 12 and 336 respectively. If one of the number is 84, the other is
The HCF of two numbers is 15 and their LCM is 225. If one of the number is 75, then the other number is :
The H.C.F. and L.C.M. of two 2- digit numbers are 16 and 480 respectively. The numbers are :
The product of two numbers is 4107. If the H.C.F. of the numbers is 37, the greater number is
The product of two numbers is 2160 and their HCF is 12. Number of such possible pairs is
The HCF of two numbers is 16 and their LCM is 160. If one of the number is 32, then the other number is
The HCF and product of two numbers are 15 and 6300 respectively. The number of possible pairs of the numbers is
The H.C.F. of two numbers is 8. Which one of the following can never be their L.C.M.?
The HCF and LCM of two numbers are 18 and 378 respectively. If one of the number is 54, then the other number is
The L.C.M. of three different numbers is 120. Which of the following cannot be their H.C.F.?
The product of two numbers is 216. If the HCF is 6, then their LCM is
|
1365 videos|1312 docs|1010 tests
|
|
1365 videos|1312 docs|1010 tests
|