MCQ: Height & Distance - 1 - SSC CGL MCQ
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ: Height & Distance - 1
The angle of elevation of the sun is 60°. Find the length of the shadow of a man who is 180 cm tall.
The stature of a tree is 10m. It is twisted by the wind in a manner that its top touches the ground and makes a point of 60 with the ground. At what range from base did the tree get twisted? (√3 = 1.73)
What is the distance between a tower and an observer if the angle of elevation from the observer’s eye to the top of the tower (height = 50 m) is 30°? The observer is 1.5 m tall.
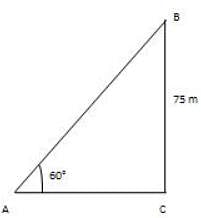
A kite is flying at a tallness of 75 m from the level of ground, joined to a string slanted at 60° to the level. The string's length is:
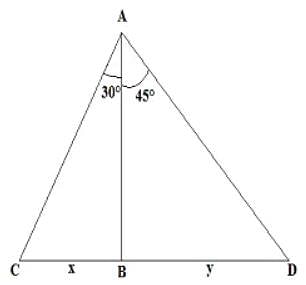
Two boats are spotted on the two sides of a light house. If the angle of depression made by both the boats from top of the lighthouse is 30° and 45° and the height of the light house is 125 m then find the distance between the two boats.
At a moment, the shadow's length of a shaft is √3 times the stature of the shaft. The edge of rise of the sun is:
A man standing on the terrace of a building watches a car speeding towards him. If at that particular instant the car is 200 m away from the building makes an angle of depression of 60° with the man’s eye and after 8 seconds the angle of depression is 30°, what is the speed of the car?
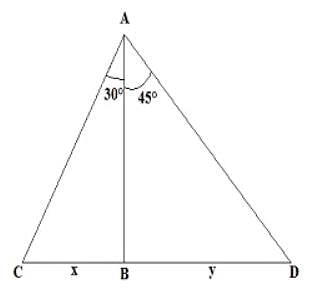
Two men are inverse sides of a tower. They gauge the edge of the rise of the highest point of the tower as 30° and 45° respectively. On the off chance that the tallness of the tower is 50 m, discover the separation between the two men. (Take √3=1.732)
A ship is approaching an observation tower. If the time taken by the ship to change the angle of elevation from 30° to 45° is 10 minutes, then find the time the ship will take to cover the remaining distance and reach the observation tower assuming the ship to be travelling at a uniform speed.
The shadow of a building is 10 m long when the point of rise of the sun is 60°. Discover the building's stature.
On the two sides of a road are two tall buildings exactly opposite to each other. The height of the taller building is 60 m. If the angle of elevation from the top of the smaller building to the top of the taller one is 30° and the angle of depression from top of the taller building to the foot of the smaller one is 30°, then find the height of the smaller building.
A straight tree is broken due to thunder storm. The broken part is bent in such a way that the peak touches the ground at an angle elevation of 45°. The distance of peak of tree (where it touches the root of the tree is 20 m. Then the height of the tree is
An observer 1.6 m tall is 20√3 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:
An aeroplane when 750 m high passes vertically above another aeroplane at an instant when their angles of elevation at same observing point are 45° and 30&de; respectively. Approximately, how many meters higher is the one than the other?
The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
|
1366 videos|1313 docs|1016 tests
|
|
1366 videos|1313 docs|1016 tests
|


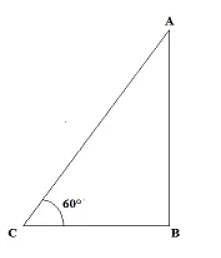
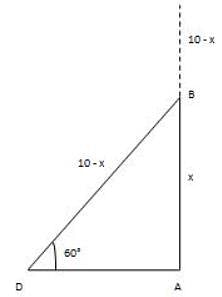

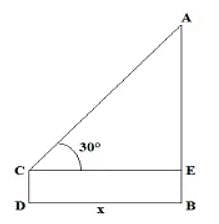
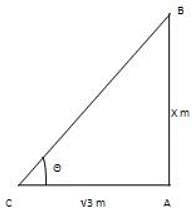
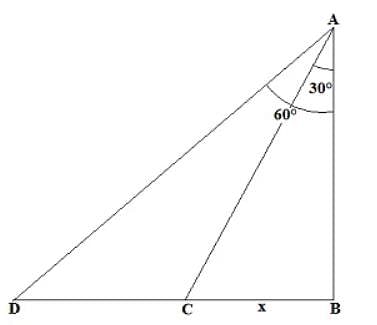
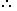 CD = BD – BC = 200 – 66.67 = 133.33 m
CD = BD – BC = 200 – 66.67 = 133.33 m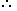 Speed = 133.33/8 = 16.67 m/s
Speed = 133.33/8 = 16.67 m/s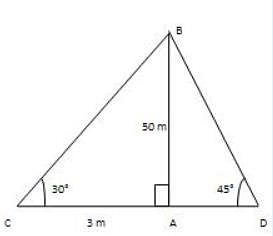





 ACB = 60º and AC = 4.6 m.
ACB = 60º and AC = 4.6 m.















