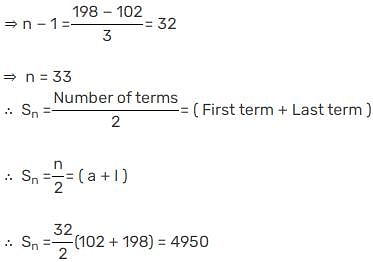MCQ: Number System - 3 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Number System - 3
When a certain number is multiplied by 13, the product consists entirely of fives. The smallest such number is ?
Every prime number of the form 3k + 1 can be represented in the form 6m + 1 (where k, m are integers), When
If the numerator of a certain fraction is increased by 2 and the denominator is increased by 1, then the resulting fraction is equal to the 1/2. If how ever the numerator is increased by 1, then denominator is decreased by 2, then the resulting fraction is equal to 3/5. Find the original fraction?
Out of three given numbers, the first number is twice the second and thrice the third. If the average of these three numbers is 154, then what is the difference between the first and the third numbers?
On children's Day, sweets were to be equally distributed amongst 300 children. But on that particular day 50 children remained absent; hence each child got one extra sweet. How many sweet were distributed?
There are two examination halls P and Q. If 10 students shifted P to Q, then the number of students will be equal in both the examination halls. If 20 students shifted from Q to P, then the students of P would be doubled to the students of Q. The number of students would be in P and Q respectively are ?
There are 200 question in a 3 hour examination. Among 200 question, 50 are Mathematics, 100 are from GK and 50 are from Sciences. Ram spent twice as much time on each Mathematics question for each other question. How many minute did he spend on Mathematics questions?
In an examination paper of five questions 5% of the candidates answered all of them and 5% answered none. Of the rest 25% candidates answered only one question and 20% answered 4 question. If 396 candidates answered either 2 question or 3 question. The number of candidates that appeared for the examination was
In a two digit positive number the unit digit is equal to the square of ten's place digit. The difference between the original number and the number formed by interchanging the digit is 54. What of 40% of the original number?
When 1/7 of a number is subtracted from the number itself, it gives the same value as the sum of all the angels of a triangle. What is the number ?
The product of two consecutive odd number is 6723. What is the greater number ?
The sum of the digits of a two-digit number is 14 and the difference between the two digits of the number is 2. What is the product of the two digits of the two-digit number ?
Find the greatest among the following given numbers.
(3)1/3, (2)1/2, 1, (6)1/6
The sum of all natural numbers between 100 and 200, which are multiples of 3 is :
In a two–digit number, the digit at the unit’s place is 1 less than twice the digit at the ten’s place. If the digits at unit’s and ten’s place are interchanged, the difference between the new and the original number is less than the original number by 20. The original number is
|
314 videos|170 docs|185 tests
|