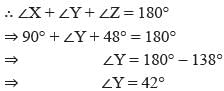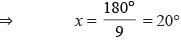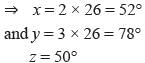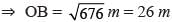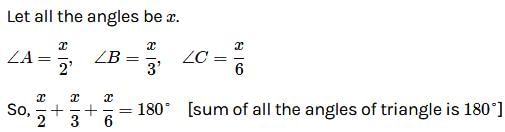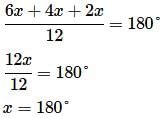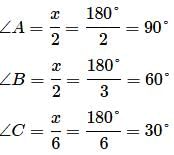Olympiad Test: Triangle - 1 - Class 7 MCQ
10 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Triangle - 1
Two angles of a triangle are equal and the third angle measures 70°. Find the measure of each of the unknown angles.
Each of the two equal angles of an isosceles triangle is twice the third angle. Find the angles of the triangle.
Find the angles of a triangle which are in the ratio 4 : 3 : 2.
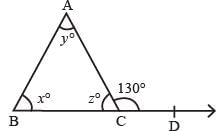
In the figure given alongside, x : y = 2 : 3 and ∠ACD = 130° find the values of x, y and z.
A man goes 24m due east and then 10m due north. How far is he away from his initial position?
The lengths of the sides of two triangles are given below. Which of them is right – angled?
(i) a = 8 cm, b = 5 cm, and c = 10 cm
(ii) a = 7 cm, b = 24 cm, and c = 25 cm
Two poles of height 9 cm and 14m stand upright on a plane ground. If the distance between their feet is 12 m. Find the distance between their tops.
In a ∆ABC it is given that ∠B = 37° and ∠C = 29°. Then ∠A = ?
|
24 videos|57 docs|100 tests
|