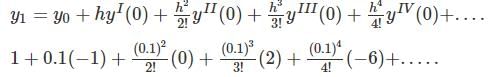Test: Mathematical Physics - 1 - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2026 - Test: Mathematical Physics - 1
The particular integral of (4D2 + 4D + 1) y = 8e-x/2 is
The value of the integral ∮₍C₎ (z² / (eⁿ + 1)) dz where C is the circle |z| = 4, is
Given vector  the line integral
the line integral 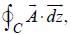 where C is a circle of radius 5 units with its center at origin is ________ ( Where dz is displacement vector)
where C is a circle of radius 5 units with its center at origin is ________ ( Where dz is displacement vector)
Consider an anti-symmetric tensor Pij with indices i and j running from 1 to 5. The number of independent components of the tensor is
Given V₁ = î - ĵ and V₂ = -2î + 3ĵ + 2k̂, which one of the following V₃ makes (V₁, V₂, V₃) a complete set for a three-dimensional real linear vector space?
Given the Legendre polynomial P0(x) = 1, P1 (x) = x and 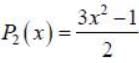 then polynomial (3x2 + x -1)
then polynomial (3x2 + x -1)
What are the order and degree respectively of the differential equation
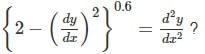
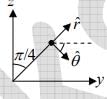
In spherical polar coordinates (r,θ,φ), the unit vector θ̂ at (10,π/4, π/2) is
Let y(x) be the solution to the differential equation 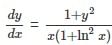 . If the value of y(1) is 0, then the value of y(e3) is
. If the value of y(1) is 0, then the value of y(e3) is
Find out the Taylor series expansion of 3 sin x + 2 cos x:
If y = y(x) is the solution of the differential equation 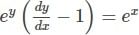 such that y(0) = 0, then y(1) is equal to
such that y(0) = 0, then y(1) is equal to
The value of the integral 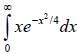 is ______ (upto two decimal places)
is ______ (upto two decimal places)
For the exact differential equation,
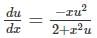
which one of the following is the solution?
The value of the Contour integral
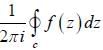
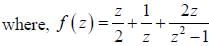
and the contour C is a circle of radius 2 centred at the origin traversed in the counterclockwise direction is ______ (answer should be an integer).
General solution of the differential equation log (dy/dx) = ax + by is
The value of y at x = 0.1 to five places of decimals, by Taylor's series method, given that dy / dx = x2y − 1,y(0) = 1, is
|
1 docs|34 tests
|


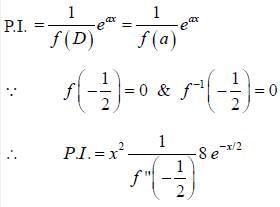
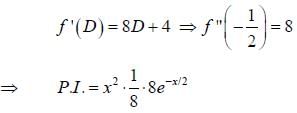
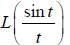

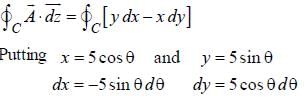
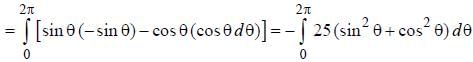
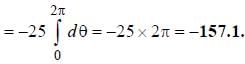
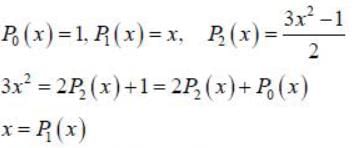
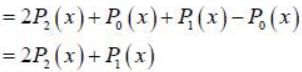
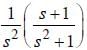
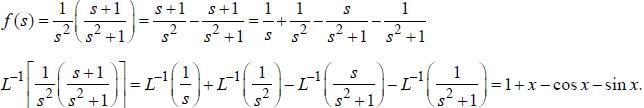
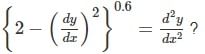
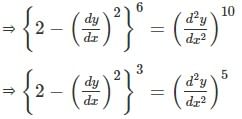

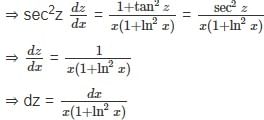
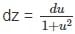
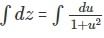
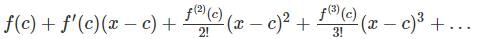
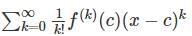
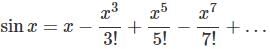


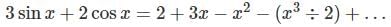
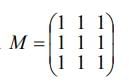
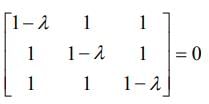
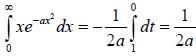
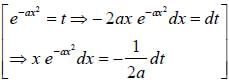
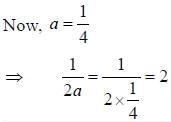
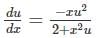
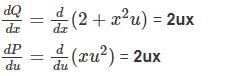
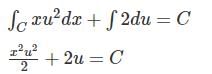
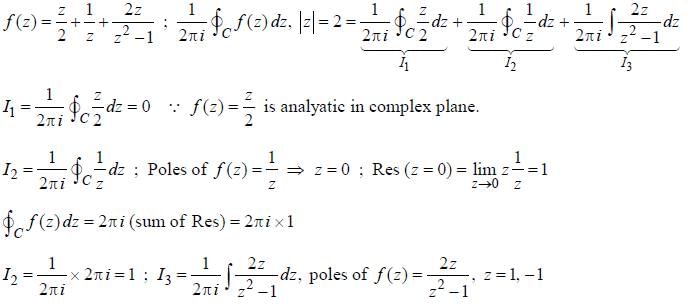
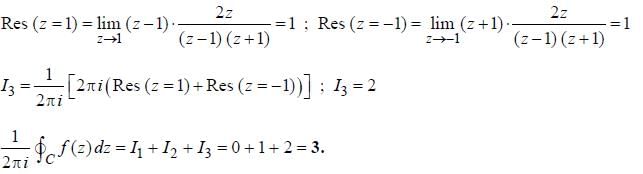
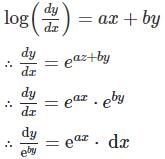
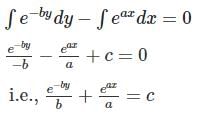
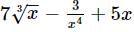 with respect x?
with respect x?