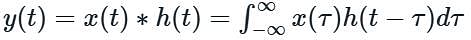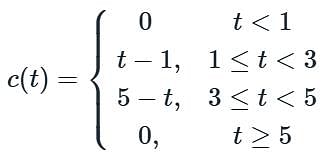Test: Continuous Time Convolution - Electrical Engineering (EE) MCQ
20 Questions MCQ Test Signals and Systems - Test: Continuous Time Convolution
Find the value of h[n]*d[n-1], d[n] being the delta function.
Find the value of h[n]*d[n-5], d[n] being the delta function.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Evaluate (exp(-4t)u(t))*u(t), u(t) being the heaviside function.
Find the convolution of x(t) = exp(2t)u(-t), and h(t) = u(t-3)
Find the value of h[n]*d[n+1], d[n] being the delta function.
Find the convolution of x(t) = exp(3t)u(-t), and h(t) = u(t-3)
Find the value of d(t-34)*x(t+56), d(t) being the delta function.
If h1, h2 and h3 are cascaded, find the overall impulse response
If h1, h2 and h3 are cascaded, and h1 = u(t), h2 = d(t) and h3 = d(t), find the overall impulse response
If h1, h2 and h3 are cascaded, and h1 = u(t+4), h2 = d(t-3) and h3 = d(t-5), find the overall impulse response
If h1, h2 and h3 are parallelly summed, find the overall impulse response
If h1, h2 and h3 are cascaded, and h1 = u(t), h2 = exp(t) and h3 = sin(t), find the overall impulse response
What is the convolution integral c(t) for a system with input x(t) and impulse response h(t), where x(t) = u(t - 1) - u(t - 3) and h(t) = u(t) - u(t - 2) ?
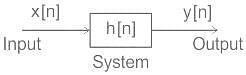
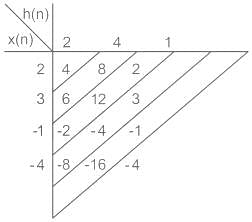
The convolution sum of x[n] and h[n] is given as:
We have x(n) = {2, 3, -1, -4} & h(n) = {2,4,1}. If y (n) is convolution of x(n) & h(n), then what is the sum of the initial and final sample of y(n)?
What is the convolution integral c(t) for a system with input x(t) and impulse response h(t), where x(t) = u(t - 1) - u(t - 3) and h(t) = u(t) - u(t - 2) ?
The convolution sum of x[n] and h[n] is given as:
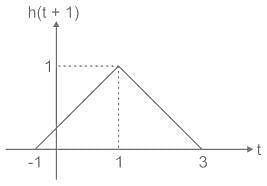
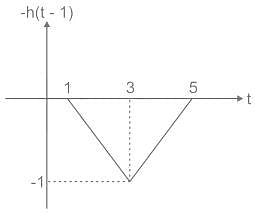
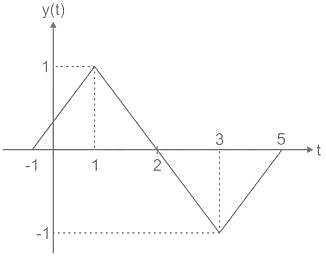
The signal x(t) and h(t) shown in the figures are convolved to yield y(t)
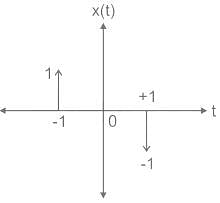
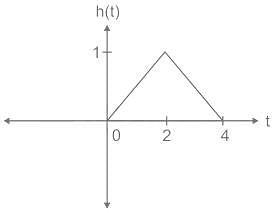
Which one of the following figures represent the output y(t)?
|
41 videos|52 docs|33 tests
|
|
41 videos|52 docs|33 tests
|