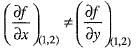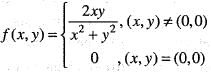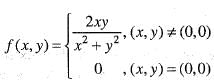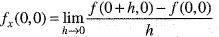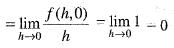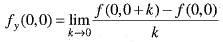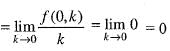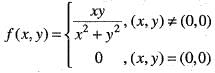Test: Functions Of One,Two Or Three Real Variables -3 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Functions Of One,Two Or Three Real Variables -3
The function f(x) = - 2x3 - 9x2 - 12x + 1 is an increasing function in the interval
If f(x) is real-valued function defined on [0, ∞] such that f(0) = 0 and 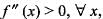 then the function h(x)
then the function h(x) 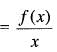 is
is
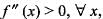 then the function h(x)
then the function h(x) 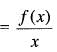 is
is f(x) = x6 - x - 1, x ∈ [1, 2], consider the following statements
(i) f is increasing on [1, 2]
(ii) f has root in [1, 2]
(iii) f is decreasing in [1, 2]
(iv) f has no root in [1 ,2]
Q. which of the above is/are correct?
(i) f is increasing on [1, 2]
(ii) f has root in [1, 2]
(iii) f is decreasing in [1, 2]
(iv) f has no root in [1 ,2]
Q. which of the above is/are correct?
The value of ‘C’ of Lagrange’s mean value theorem for f( x ) = x (x - 1) in [1 ,2] is given by
Let
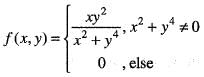
Then, the directional derivative at c = (0, 0) in the direction u = (a1, a2) is
The derivative of the function f(x) = x2m is
Let f(x) = | sin πx |, 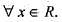 then
then
If f'(a) exists, then 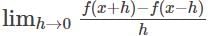 is equal to
is equal to
A function is said to be ______________ if and only if f(a) = f(b) implies that a = b for all a and b in the domain of f.
The continuous function f : R -->R defined by f(x) = (x2 + 1)2011 is
Let
f(x, y) = 2x2 - xy + 2y2 Then at (1, 2)
If any four numbers are selected and they are multiplied, then the probability that the last digit will be 1, 3, 5 or 7 is
Let
f(x,y) = x3 + y3- 63 (x + y) + 12xy,
then
|
27 docs|150 tests
|


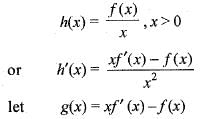
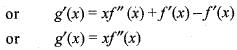
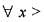 0 => g (x) is strictly increasing function in [0, ∞]
0 => g (x) is strictly increasing function in [0, ∞]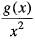
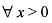

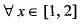
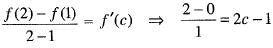 or 2 = 2c - 1
or 2 = 2c - 1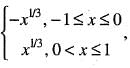 then
then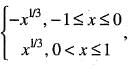
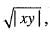 then
then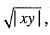
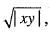
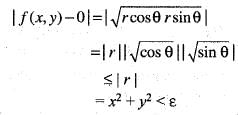
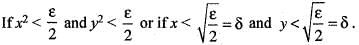 Hence for given ε > 0, there exists δ > 0 such that
Hence for given ε > 0, there exists δ > 0 such that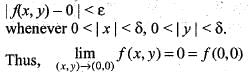 Therefore, f(x, y) is continuous at (0, 0). Hence option (a) is correct.
Therefore, f(x, y) is continuous at (0, 0). Hence option (a) is correct.
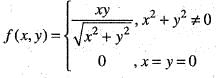
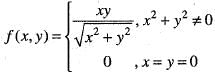

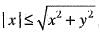
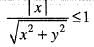
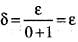
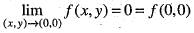
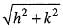 •
• 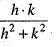
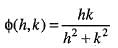
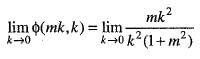
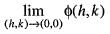 does not exists. Hence, f(x, y) is not differentiable at origin. Hence, option (b) is incorrect.
does not exists. Hence, f(x, y) is not differentiable at origin. Hence, option (b) is incorrect.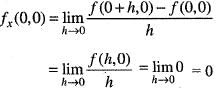 Hence, option (c) is incorrect.
Hence, option (c) is incorrect.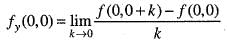
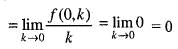
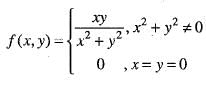
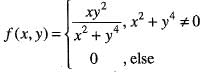
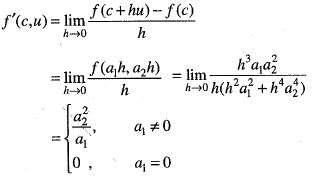
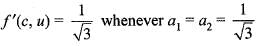
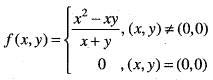
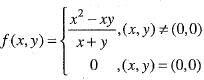
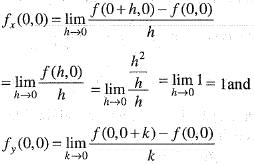
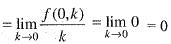
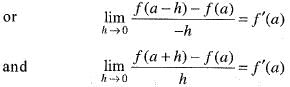 Adding these two, we get
Adding these two, we get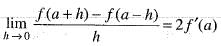
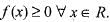 therefore is not onto and f(- 1) = f(1) , therefore, f(x) is not one-one.
therefore is not onto and f(- 1) = f(1) , therefore, f(x) is not one-one.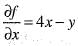
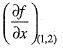 = 4 x 1 - 2 = 2
= 4 x 1 - 2 = 2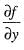 = - x + 4y
= - x + 4y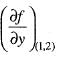 = - l + 4x 2 = 7
= - l + 4x 2 = 7