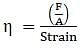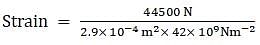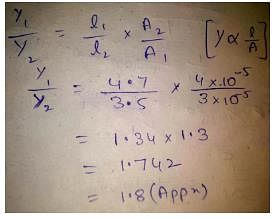Test: Mechanical Properties of Solids - NEET MCQ
30 Questions MCQ Test Physics Class 11 - Test: Mechanical Properties of Solids
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2 . It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the resulting strain. Young's Modulus of Steel (Y) = 20×1010 Pa
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain? Take Young's modulus of copper as 42 × 109Pa
What diameter should a 10-m-long steel wire have if we do not want it to stretch more than 0.5 cm under a tension of 940 N? Take Young's modulus of steel as 20 × 1010 Pa
Elasticity is the property of a body, by virtue of which
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2. It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the elongation. Take Young's modulus of steel as 20 × 1010 Pa
A 200-kg load is hung on a wire with a length of 4.00 m, a cross-sectional area of 0.200 × 10−4 m2, and a Young’s modulus of 8.00 × 1010N/ m2. What is its increase in length?
The importance of the elastic behavior of materials is
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm. Bulk modulus of glass 37 GPa.
If the elastic limit of copper is 1.5 × 108 N/ m2, determine the minimum diameter a copper wire can have under a load of 10.0 kg if its elastic limit is not to be exceeded.
Rectangular section is rarely used in beams because
A circular steel wire 2.00 m long must stretch no more than 0.25 cm when a tensile force of 400 N is applied to each end of the wire. What minimum diameter is required for the wire?
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10−2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire were twice as long?
In constructing a large mobile, an artist hangs an aluminum sphere of mass 6.0 kg from a vertical steel wire 0.50 m long and 2.5 × 10−3 cm2in cross-sectional area. On the bottom of the sphere he attaches a similar steel wire, from which he hangs a brass cube of mass 10.0 kg. Compute the elongation.
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10−5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10−5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
A lead cube measures 6.00 cm on each side. The bottom face is held in place by very strong glue to a flat horizontal surface, while a horizontal force F is applied to the upper face parallel to one of the edges. How large must F be to cause the cube to deform by 0.250 mm? (Shear modulus of lead = 0.6 × 1010Pa)
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107Pa? Assume that each rivet is to carry one quarter of the load.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?
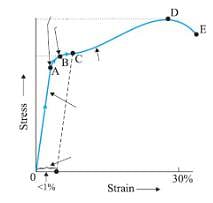
With reference to figure the elastic zone is
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched for a copper wire of the original length and diameter?
|
97 videos|378 docs|103 tests
|