Get the App Signup / Login

Class 9 Exam > Class 9 Tests > Mathematics (Maths) Class 9 > Test: Circles- 1 - Class 9 MCQ

Test: Circles- 1 - Class 9 MCQ

Test Description

25 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Circles- 1

Test: Circles- 1 for Class 9 2024 is part of Mathematics (Maths) Class 9 preparation. The Test: Circles- 1 questions and answers have been prepared according to the Class 9 exam syllabus.The Test: Circles- 1 MCQs are made for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Circles- 1 below.

Solutions of Test: Circles- 1 questions in English are available as part of our Mathematics (Maths) Class 9 for Class 9 & Test: Circles- 1 solutions in Hindi for Mathematics (Maths) Class 9 course. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free. Attempt Test: Circles- 1 | 25 questions in 25 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study Mathematics (Maths) Class 9 for Class 9 Exam | Download free PDF with solutions

Test: Circles- 1 - Question 1

Save

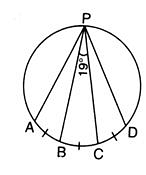
In the given figure, ∠BPC = 19^o, arc AB = arc BC = arc CD. Then, the measure of ∠APD is

A.
59^o
B.
58^o
C.
76^o
D.
38^o

Detailed Solution for Test: Circles- 1 - Question 1

If arc AB = arc BC = arc CD
then , angle suspended on circle is also equal
So, Sum of all angle is equal to angle APD
Angle APB+ BPC + CPD = angle APD
19 + 19 +19 = 58^o

Test: Circles- 1 - Question 2

Save

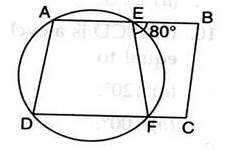
ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80^o, then ∠ABC is equal to

A.
120^o
B.
100^o
C.
80^o
D.
75^o

Detailed Solution for Test: Circles- 1 - Question 2

Given, ABCD is a parallelogram and AEFD is a cyclic quadrilateral.
∠BEF=80^∘
Now, ∠ADC=∠BEF=80^∘ (Angle of a cyclic quadrilateral is equal to the opposite exterior angle )
Also, now in parallelogram ABCD,
∠ABC=∠ADC=80^∘ (Opposite angles of a parallelogram are equal)

1 Crore+ students have signed up on EduRev. Have you? Download the App

Test: Circles- 1 - Question 3

Save

In the given figure, ABCD is a quadrilateral inscribed in circle with centre O. CD is produced to E. If ∠ADE = 95^o and ∠OBA = 30^o, then ∠OAC is equal to

A.
20^o
B.
15^o
C.
10^o
D.
5^o

Detailed Solution for Test: Circles- 1 - Question 3

Test: Circles- 1 - Question 4

Save

In a figure, O is the centre of the circle with AB as diameter. If ∠AOC = 40^o, the value of x is equal to

A.
80^o
B.
70^o
C.
50^o
D.
60^o

Detailed Solution for Test: Circles- 1 - Question 4

The value of x is equal to 70°.

Since AB is the diameter, angle AOC is a central angle and its value is twice the inscribed angle subtended by the same chord. Therefore, x = 2 * 35° = 70°.

Test: Circles- 1 - Question 5

Save

The given figures show two congruent circles with centre O and O’. Arc AXB subtends an angle of 75^o at the centre and arc A’YB’ subtends an angle of 25^o at the centre O’. Then, the ratio of arcs AXB to A ‘YB’ is

A.
it is 3 : 1
B.
it is 1 : 3
C.
it is 1 : 2
D.
it is 2 : 1

Detailed Solution for Test: Circles- 1 - Question 5

Because the circles are congruent, therefore their radius are same

Length of arc AXB = [θ/(360°)] × 2πr = [(75°)/(360°)] × 2πr

Length of arc A’YB’ = [θ/(360°)] × 2πr = [(25°)/(360°)] × 2πr

Required Ratio = ([(75°)/(360°)] × 2πr) : ([(25°)/(360°)] × 2πr) = 3 : 1

Test: Circles- 1 - Question 6

Save

If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is

A.
45^o
B.
30^o
C.
60^o
D.
90^o

Test: Circles- 1 - Question 7

Save

The given figure shows two intersecting circles. If ∠ABC = 75^o, then the measure of ∠PAD is

A.
75^o
B.
125^o
C.
105^o
D.
150^o

Test: Circles- 1 - Question 8

Save

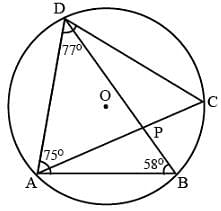
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75^o, ∠ABD = 58^o and ∠ADC = 77^o , AC and BD intersect at P. the measure of ∠DPC is

A.
92^o
B.
105^o
C.
90^o
D.
94^o

Detailed Solution for Test: Circles- 1 - Question 8

∠DBA = ∠DCA = 58° …(1)

[Angles in same segment] ABCD is a cyclic quadrilateral :

Sum of opposite angles = 180 degrees

∠A +∠C = 180°

75° + ∠C = 180°

∠C = 105°

Again,

∠ACB + ∠ACD = 105°

∠ACB + 58° = 105°

or ∠ACB = 47° …(2)

Now, ∠ACB = ∠ADB = 47° [Angles in same segment]

Also, ∠D = 77° (Given)

Again From figure, ∠BDC + ∠ADB = 77°

∠BDC + 47° = 77°

∠BDC = 30°

In triangle DPC

∠PDC + ∠DCP + ∠DPC = 180°

30° + 58° + ∠DPC = 180°

or ∠DPC = 92°

Test: Circles- 1 - Question 9

Save

For what value of x in the figure, points A, B, C and D are concyclic ?

A.
9^o
B.
12^o
C.
11^o
D.
10^o

Test: Circles- 1 - Question 10

Save

Greatest chord of a circle is called its

A.
chord
B.
secant
C.
radius
D.
diameter

Test: Circles- 1 - Question 11

Save

In the given figure PQ and RS are two equal chords of a circle with centre O. OA and OB are perpendiculars on chords PQ and RS, respectively. If ∠AOB = 140^o, then ∠PAB is equal to

A.
40^o
B.
70^o
C.
60^o
D.
50^o

Test: Circles- 1 - Question 12

Save

In the given figure, chords AB and CD intersect at P. If ∠DPB = 88^o and ∠DAP = 46^o, then the measure of ∠ABC is

A.
48^o
B.
44^o
C.
42^o
D.
46^o

Test: Circles- 1 - Question 13

Save

AD is diameter of a circle and AB is a chord. If AD = 50 cm, AB = 48 cm, then the distance of AB from the centre of the circle is

A.
6 cm
B.
8 cm
C.
5 cm
D.
7 cm

Test: Circles- 1 - Question 14

Save

In the given figure, O is the centre of the circle. If ∠CAB = 40^o and ∠CBA = 110^o, the value of x is :

A.
80^o
B.
55^o
C.
60^o
D.
50^o

Test: Circles- 1 - Question 15

Save

Angle formed in minor segment of a circle is

A.
a straight angle
B.
an acute angle
C.
a right angle
D.
an obtuse angle

Test: Circles- 1 - Question 16

Save

In the given figure PQ = QR = RS and ∠PTS = 75^o then the measure of ∠QOR is

A.
25^o
B.
20^o
C.
50^o
D.
75^o

Test: Circles- 1 - Question 17

Save

In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95^o then ∠AOD is equal to

A.
190^o
B.
170^o
C.
180^o
D.
175^o

Test: Circles- 1 - Question 18

Save

The given figure shows two congruent circles with centre O and O’ intersecting at A and B. If ∠AO′B = 50^o, then the measure of ∠APB is

A.
45^o
B.
25^o
C.
40^o
D.
50^o

Test: Circles- 1 - Question 19

Save

Angle inscribed in a semicircle is :

A.
60^o
B.
90^o
C.
75^o
D.
120^o

Detailed Solution for Test: Circles- 1 - Question 19

Test: Circles- 1 - Question 20

Save

Number of circles that can be drawn through three non-collinear points is

A.
3
B.
1
C.
2
D.
0

Test: Circles- 1 - Question 21

Save

In the given figure, if ∠ABC = 50^o and ∠BDC = 40^o, then ∠BCA is equal to

A.
90^o
B.
50^o
C.
100^o
D.
40^o

Test: Circles- 1 - Question 22

Save

In the given figure, chords AB and CD intersect each other at right angles. Then, ∠x+∠y is equal to

A.
75^o
B.
90^o
C.
45^o
D.
60^o

Test: Circles- 1 - Question 23

Save

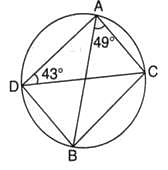
In the given figure if ∠CAB = 49^o and ∠ADC = 43^o, then the measure of ∠ACB is

A.
92^o
B.
88o
C.
74^o
D.
96^o

Test: Circles- 1 - Question 24

Save

In the given figure, O is the centre of the circle. If ∠QPR is 50^o, then ∠QOR is :

A.
130^o
B.
50^o
C.
100^o
D.
40^o

Test: Circles- 1 - Question 25

Save

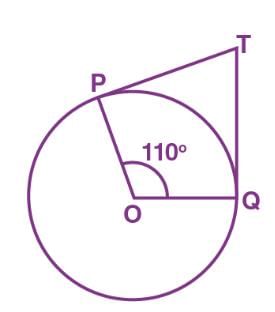
If TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to

A.
60°
B.
70°
C.
80°
D.
90°

Detailed Solution for Test: Circles- 1 - Question 25

As per the given question:

We can see, OP is the radius of the circle to the tangent PT and OQ is the radius to the tangents TQ.

So, OP ⊥ PT and TQ ⊥ OQ

∴ ∠OPT = ∠OQT = 90°

Now, in the quadrilateral POQT, we know that the sum of the interior angles is 360°

So, ∠PTQ + ∠POQ + ∠OPT + ∠OQT = 360°

Now, by putting the respective values, we get,

⇒ ∠PTQ + 90° + 110° + 90° = 360°

⇒ ∠PTQ = 70°

	Mathematics (Maths) Class 9 44 videos\|412 docs\|55 tests

Mathematics (Maths) Class 9

44 videos|412 docs|55 tests

Join Course

Information about Test: Circles- 1 Page

In this test you can find the Exam questions for Test: Circles- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Circles- 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 9

	Mathematics (Maths) Class 9 44 videos\|412 docs\|55 tests

Mathematics (Maths) Class 9

44 videos|412 docs|55 tests

Join Course

Download as PDF

Top Courses for Class 9

Join with a free account

Get Instant Access to 1000+ FREE Docs, Videos & Tests

10,000,000

Users

100+

Exams

3,25,000

Docs and Videos

75,000

Tests

I have an EduRev Account • Sign Up with Email

Attempt this test on App!

Get detailed analysis along with solutions of each question.

Open in App

Not Now

Schools

Medical
Non- Medical
Commerce
Humanities
CBSE Class 10
CBSE Class 9
CBSE Class 8
CBSE Class 7
CBSE Class 6
CBSE Class 5
CBSE Class 4
CBSE Class 3
CBSE Class 2
CBSE Class 1

Competitive Examinations

UPSC
NEET
JEE
CLAT
CAT
GMAT
GATE
Railways
SSC
IIT JAM
Defence
Insurance
Teaching
CA Foundation

Technical Exams

GATE
SSC JE
RRB JE
Civil Engineering
Computer Science Engineering
Electrical Engineering
Electronics Engineering
Biotechnology Engineering
Mechanical Engineering
Chemical Engineering

Important Questions for Circles- 1

Find all the important questions for Circles- 1 at EduRev.Get fully prepared for Circles- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Circles- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Circles- 1 resources.

Circles- 1 MCQs with Answers

Prepare for the Circles- 1 within the Class 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Circles- 1 Mathematics (Maths) Class 9

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Circles- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.

Education Revolution

Free Exam Preparation
at your Fingertips!

Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

Signup now for free

Join the 10M+ students on EduRev

Get the EduRev App

Scan this QR code to
download the app for Free

Or check it out in the app stores

Welcome Back

Continue with Facebook

Forgot Password?

New User? Sign Up

Test: Circles- 1 - Class 9 MCQ

25 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Circles- 1

In the given figure, ∠BPC = 19o, arc AB = arc BC = arc CD. Then, the measure of ∠APD is

ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80o, then ∠ABC is equal to

In the given figure, ABCD is a quadrilateral inscribed in circle with centre O. CD is produced to E. If ∠ADE = 95o and ∠OBA = 30o, then ∠OAC is equal to

Mathematics (Maths) Class 9

Top Courses for Class 9

Mathematics (Maths) Class 9

Top Courses for Class 9

Important Questions for Circles- 1

Circles- 1 MCQs with Answers

Online Tests for Circles- 1 Mathematics (Maths) Class 9

In the given figure, ∠BPC = 19^o, arc AB = arc BC = arc CD. Then, the measure of ∠APD is

ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80^o, then ∠ABC is equal to

In the given figure, ABCD is a quadrilateral inscribed in circle with centre O. CD is produced to E. If ∠ADE = 95^o and ∠OBA = 30^o, then ∠OAC is equal to