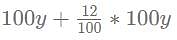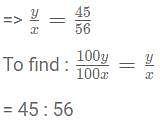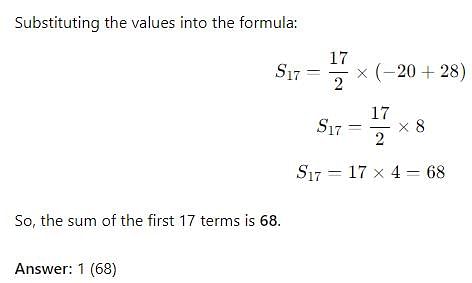Practice Test: Quantitative Aptitude - 13 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2025 - Practice Test: Quantitative Aptitude - 13
Given that x3 + y3 = 72 and xy = 8 with x > y. Then the value of (x - y) is
The graphs of x = a and y = b intersect at
If sum of the roots of a quadratic equation is 7 and product of the roots is 12. Find the quadratic equation.
The area of the triangle formed by the graphs of the equations x = 0, 2x + 3y = 6 and x + y = 3 is:
Which value among 3√5, 4√6, 6√12, 12√276 is the largest?
I multiplied a natural number by 18 and another by 21 and added the products. Which one of the following could be the sum?
Which one of the following will completely divide 571 + 572 + 573?
A certain number when divided by 899 leaves the remainder 65. When the same number is divided by 31, the remainder is:
By what least number should 675 be multiplied to obtain a number which is a perfect cube?
A manufacturer marked an article at Rs. 50 and sold it allowing 20% discount. If his profit was 25%, then the cost price of the article was
If a trader sold an article at Rs.3,060 after allowing 15% and 10% successive discounts on marked price, then the marked price is
By selling an article, a man makes a profit of 25% of its selling price. His profit percent is
A starts business with Rs. 7000 and after 5 months. B joined as a partner. After a year the profit is divided in the ratio 2 : 3. The capital of B is:
A shopkeeper earns a profit of 12% on selling a book at 10% discount on printed price. The ratio of the cost price to printed price of the book is
If the 3rd and the 5th term of an arithmetic progression are 13 and 21, what is the 13th term?
What is the sum of the first 12 terms of an arithmetic progression if the first term is -19 and last term is 36?
What is the sum of the first 17 terms of an arithmetic progression if the first term is -20 and last term is 28?
The 3rd and 8th term of an arithmetic progression are -13 and 2 respectively. What is the 14th term?
The 4th and 7th term of an arithmetic progression are 11 and -4 respectively. What is the 15th term?
|
237 docs|133 tests
|


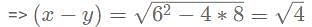
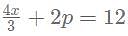 for what value of p, x = 6?
for what value of p, x = 6?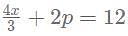

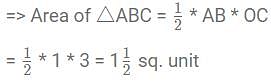
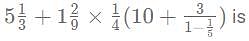
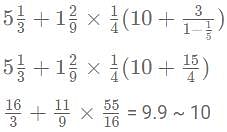
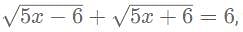 then what is the value of x?
then what is the value of x?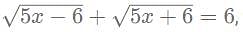
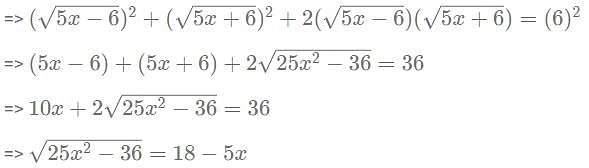
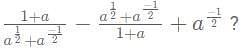
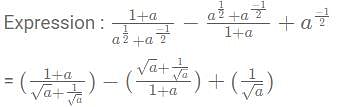
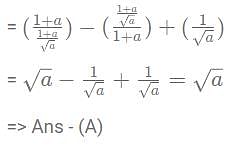
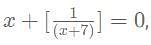 then what is the value of
then what is the value of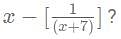
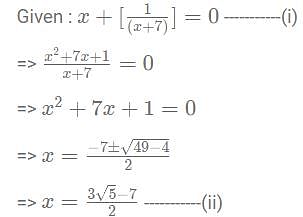
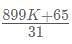 = Remainder of 65/31 as 899 is completely divisible by 31
= Remainder of 65/31 as 899 is completely divisible by 31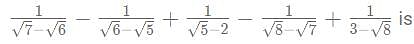
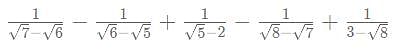
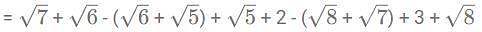
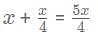
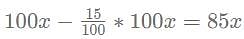
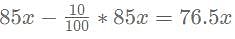
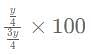
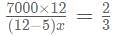
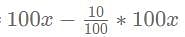 = 90x
= 90x