Assertion & Reason Test: Probability - 1 - Class 10 MCQ
10 Questions MCQ Test - Assertion & Reason Test: Probability - 1
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Let A and B be two independent events.
Assertion : If P (A) = 0.3 and P (A ∪ 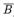 ) = 0.8, then P (B) is 2/7.
) = 0.8, then P (B) is 2/7.
Reason : P (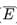 ) = 1 - P(E), where E is any event.
) = 1 - P(E), where E is any event.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : When two coins are tossed simultaneously then the probability of getting no tail is 1/4.
Reason : The probability of getting a head (i.e., no tail) in one toss of a coin is 1/2.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: If the probability of an event is P then probability of its complementary event will be 1 - P.
Reason: When E and 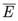 are complementary events, then P (E) + P(
are complementary events, then P (E) + P(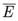 ) = 1.
) = 1.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : In a simultaneous throw of a pair of dice. The probability of getting a double is 1/6.
Reason: Probability of an event may be negative.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : The probability of winning a game is 0.4, then the probability of losing it, is 0.6
Reason : P(E) + P(not E) = 1
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : Cards numbered as 1, 2, 3 .......... 15 are put in a box and mixed thoroughly, one card is then drawn at random. The probability of drawing an even number is 1/2.
Reason : For any event E, we have 0 ≤ P(E) ≤ 1
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : If E and F are events such that P(E) = 1/4, P(F) = 1/2 and P(E and F) = 1/8, then P (E or F) is 5/8.
Reason : If A and B are independent, then P (A ∩ B) = P (A).
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: The probabilities that A, B, C can solve a problem independently are 1/3, 1/3 and 1/4 respectively. The probability that only two of them are able to solve the problem is 7/36.
Reason : If A and B are mutually exclusive events, then P(A ∩ B) ≠ 0.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If P(F) = 0.20, then the probability of ‘not E’ is 0.80.
Reason (R): If two dice are thrown together, then the probability of getting a doublet is 5/6.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The probability that a number selected at random from the number 1, 2, 3, ......., 15 is a multiple of 4, is 1/3.
Reason (R): Two different coins are tossed simultaneously. The probability of getting at least one head is 3/4.














