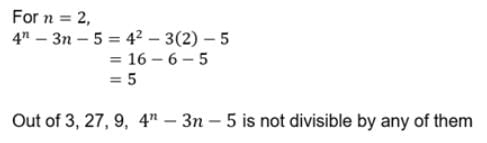Test: Principle Of Mathematical Induction- 1 - Commerce MCQ
25 Questions MCQ Test Online MCQ Tests for Commerce - Test: Principle Of Mathematical Induction- 1
Let P(n) be a statement and let P(n)⇒P(n+1) for all natural numbers n, then P(n) is true for
Let P(n) be a statement 2n<n!, where n is a natural number, then P(n) is true for
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If x > -1, then the statement (1+x)n>1+nx is true for
The smallest +ve integer n , for whichn!
If P (n) = 2+4+6+………………..+2n , n ∈ N , then P (k) = k (k + 1) + 2 ⇒ P (k + 1) = (k + 1) (k +2) + 2 for all k ∈ N. So we can conclude that P (n) = n (n + 1) +2 for
x(xn-1 - nan-1)+ an (n-1) is divisible by (x-a)2 for
The greatest positive integer, which divides n (n + 1) (n + 2) (n + 3) for all n ∈ N, is
Let P (n) denote the statement n2+n is odd, It is seen that P(n) ⇒ P(n+1), therefore P (n) is true for all
The greatest positive integer, which divides (n+1)(n+2)(n+3)..................(n+r) ∀n∈W, is
The statement P (n) : “1 X 1! + 2 X 2! + 3 X 3! + …..+ n X n! = (n + 1) !..... 1 “ is
A student was asked to prove a statement P (n) by method of induction. He proved that P (3) is true and that P(n) ⇒ P(n+1) for all natural numbers n. On the basis of this he could conclude that P (n) is true
32n+2−8n−9is divisible by 64 for all
The statement 2n+2<3n is true for all
The smallest positive integer for which The statement 3n+1<4n is true for
For all n ∈ N , 49n+16n−1 is divisible by
The digit in the unit’s place of the number 183! + 3183 is
If n is a positive integer , then 2.7n+3.5n−5 is divisible by
If n is a +ve integer, then 4n−3n−5 is divisible by
If n is a +ve integer, then 2.42n+1+33n+1 is divisible by
If n is a +ve integer, then 10n +3.4n+2 + 5 is divisible by
|
705 tests
|