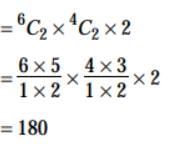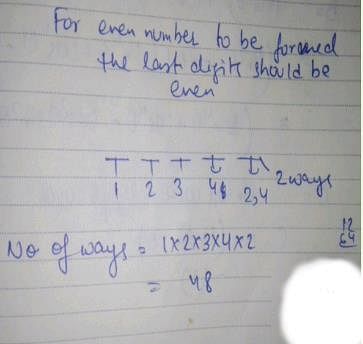Test: Permutations And Combinations - 1 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Permutations And Combinations - 1
The number of different ways in which a man can invite one or more of his 6 friends to dinner is
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In how many ways can a mixed doubles tennis game be arranged from a group of 10 players consisting of 6 men and 4 women
The number of significant numbers which can be formed by using any number of the digits 0, 1, 2, 3, 4 but using each not more than once in each number is
Numbers greater than 1000 but not greater than 4000 are to be formed with the digits 0, 1, 2, 3, 4, allowing repetitions, the number of possible numbers is
The number of all three digit even numbers such that if 5 is one of the digits then next digit is 7 is
A coin is tossed n times, the number of all the possible outcomes is
The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is
The number of ways in which the 6 faces of a cube can be painted with 6 different colours is
The number of ways in which the 4 faces of a regular tetrahedron can be painted with 4 different colours is
The number of ways in which n ties can be selected from a rack displaying 3n different ties is
Find Rank of word ‘wife ‘among the words that can be formed with its letters and arranged as in dictionary is
The number of even numbers that can be formed by using all the digits 1, 2, 3, 4, and 5 (without repetitions) is
The number of all numbers that can be formed by using some or all of the digits 1, 3, 5, 7, 9 (without repetitions) is
In a multiple choice question, there are 4 alternatives, of which one or more are correct. The number of ways in which a candidate can attempt this question is
In how many ways can the letters of the word ‘MATHEMATICS ‘be permuted so that consonants always occur together?
The number of triangles that can be formed with 6 points on a circle is
Number of ways in which 10 different things can be divided into two groups containing 6 and 4 things respectively is
The number of selections of n different things taken r at a time which exclude a particular thing is
The number of arrangements of n different things taken r at a time which include a particular thing is
The number of arrangements of n different things taken r at a time which exclude a particular thing is
5 persons board a lift on the ground floor of an 8 storey building. In how many ways can they leave the lift?
If C(12,4) + C(12,5) = C(n,5) ,then n is equal to
The number of ways in which a necklace can be formed by using 5 identical red beads and 6 identical white beads is:
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|