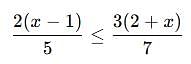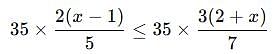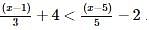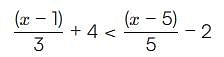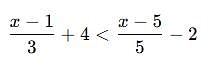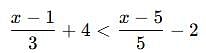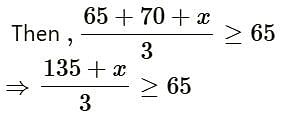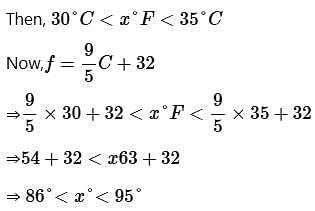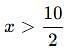Test: Linear Inequalities- 1 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Linear Inequalities- 1
By solving the inequality 3(a - 6) < 4 + a, the answer will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the first four papers each of 100 marks, Rishi got 95, 72, 73, 83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper .
A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3 cm longer than the shortest and third length is to be twice as long as the shortest. What are the possible lengths for the shortest board if the third piece is to be at least 5 cm longer than the second?
Find all pairs of consecutive odd natural numbers, both of which are larger than 10, such that their sum is less than 40.
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of atleast 65 marks.
A solution is to be kept between 30∘C and 35∘C What is the range of temperature in degree Fahrenheit?
The longest side of a triangle is three times the shortest side and the third side is 2cm shorter than the longest side if the perimeter of the triangles at least 61cm, find the minimum length of the shortest side.
Given that x is an integer, find the values of x which satisfy both 2x + 3 > 7 and x + 4 < 10
What are the integer values of x which satisfy the inequalities x > − 2 and x ≤ 2?
Given that x is an integer, find the values of x which satisfy the simultaneous linear inequalities 2 + x < 6 and 2 −3x < − 1.
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|