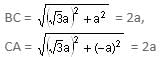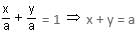Test Level 2: Coordinate Geometry - 1 (September 9) - CAT MCQ
10 Questions MCQ Test - Test Level 2: Coordinate Geometry - 1 (September 9)
The following points A (2a, 4a), B (2a, 6a) and C (2a +√3a, 5a) (a > 0) are the vertices of
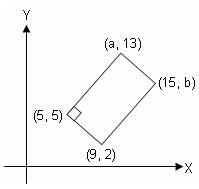
In the rectangle shown below, the value of a - b is

A straight line passing through the point of intersection of the straight lines x - 3y + 1 = 0 and 2x + 5y - 9 = 0 having infinite slope and at a distance of 2 units from the origin, has the equation
The equation of the line, which passes through the point (1, -2) and cuts off equal intercepts from the axis, is
A line intersects x-axis at A(10, 0) and y-axis at B(0, 10). Find the equation of the line.
The equation of the line passing through the point of intersection of the lines 4x - 3y - 1 = 0 and 5x - 2y - 3 = 0 and parallel to the line 2y - 3x + 2 = 0, is
The coordinates of four points are P(0, -3), Q(6, 1), R(-4, -4) and S(5, 2). Find out which line segments are parallel to each other.
Line m is the graph of the equation 2x + 3y = 7. If the point at which m crosses the y-axis has coordinates (0, k), what is the value of k?
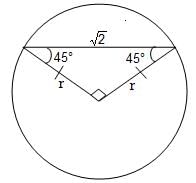
The area of the circle in which a chord of length √2 makes an angle π/2 at the centre is
Find the value of k, for the three lines x + y - 4 = 0, 3x + 2 = 0 and x - y + 3k = 0 to be concurrent