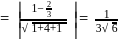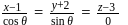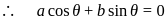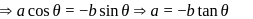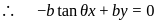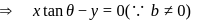3-D Geometry: Planes in Space(15 Dec) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - 3-D Geometry: Planes in Space(15 Dec)
Let A(4, 7, 8), B(2, 3, 4), C(2, 5, 7) be the vertices of a triangle ABC. The length of internal bisector of ∠A is
The length of perpendicular from the origin to the plane which makes intercepts 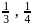 and
and 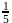 respectively on the coordinate axes is
respectively on the coordinate axes is
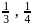 and
and 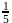 respectively on the coordinate axes is
respectively on the coordinate axes is| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A variable plane passes through a fixed point  . The locus of the foot of the perpendicular from the origin to this plane is given by
. The locus of the foot of the perpendicular from the origin to this plane is given by
 . The locus of the foot of the perpendicular from the origin to this plane is given by
. The locus of the foot of the perpendicular from the origin to this plane is given byIf Q is the image of the point P(2, 3, 4) under the reflection in the plane x − 2y + 5z = 6, then the equation of the line PQ is
The planes 3x − y + z + 1 = 0, 5x + y + 3z = 0 intersect in the line PQ. The equation of the plane through the point (2,1,4) and the perpendicular to PQ is
If from a point P(a,b,c) perpendiculars PA and PB are drawn to yz and zx planes, then the equation of the plane OAB is
Under what condition do the planes bx − ay = n, cy − bz = l, az − cx = m intersect in a line?
A plane passes through a fixed point (a,b,c) The locus of the foot of the perpendicular to it from the origin is the sphere
What is the distance between the planes x − 2y + z−1 = 0 and −3x + 6y − 3z + 2 = 0?
What is the equation of the plane through 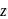 -axis and parallel to the line
-axis and parallel to the line 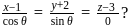
|
360 tests
|


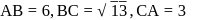
 Coordinate of
Coordinate of  are
are 
 Length
Length 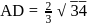
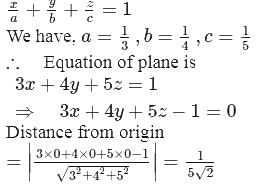
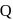 be the image of the point
be the image of the point 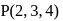 in the plane
in the plane 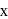
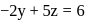 , then
, then 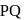 is normal to the plane ∴ direction ratios of
is normal to the plane ∴ direction ratios of 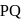 are
are 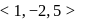 Since
Since  passes through
passes through 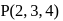 and has direction ratios
and has direction ratios 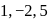
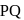 is
is 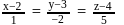
 i.e
i.e 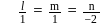
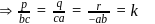
 be the fixed point on the variable plane
be the fixed point on the variable plane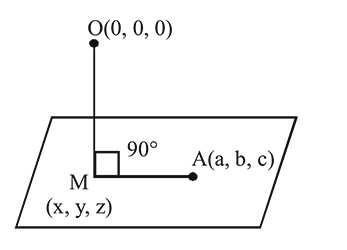
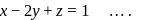
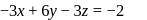
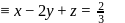
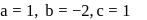
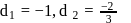
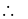 Distance
Distance