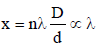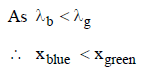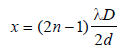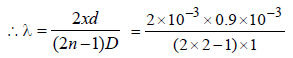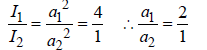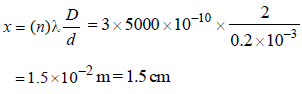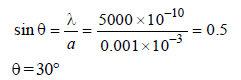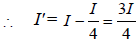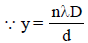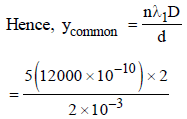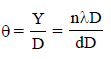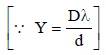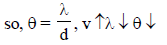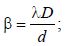31 Year NEET Previous Year Questions: Wave Optics
21 Questions MCQ Test Physics Class 12 | 31 Year NEET Previous Year Questions: Wave Optics
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which one of the following phenomena is notexplained by Huygen’s construction ofwavefront? [1988]
Huygen's construction of wavefront does not apply to origin of spectra which is explained by quantum theory
Which of the following phenomenon is notcommon to sound and light waves ? [1988]
Sound waves can not be polarised as they are longitudinal. Light waves can be polarised as they are transverse.
Interference is possible in [1989]
Interference is a wave phenomenon shown by both the light waves and sound waves.
The Young’s double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then [1990]
Distance of nth maxima, 
In Young’s double slit experiment, the fringe width is found to be 0.4 mm. If the whole apparatus is immersed in water of refrative index 4/3, without disturbing the geometrical arrangement, the new fringe width will be [1990]
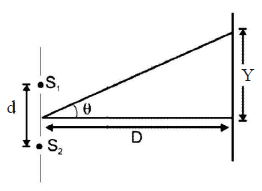
In Young’s experiment, two coherent sources areplaced 0.90 mm apart and fringe are observedone metre away. If it produces second dark fringeat a distance of 1 mm from central fringe, thewavelength of monochromatic light used wouldbe [1991, 1992]
For dark fringe
λ = 0.6x10-6 m = 6 × 10–5 cm
Ratio of intensities of two waves are given by 4 : 1. Then the ratio of the amplitudes of the twowaves is [1991]
In Young’s double slit experiment carried out withlight of wavelength (λ) = 5000Å, the distancebetween the slits is 0.2 mm and the screen is at 200 cm from the slits. The central maximum is at x = 0. The third maximum (taking the central maximum as zero th maximum) will be at x equal to [1992]
If yellow light emitted by sodium lamp in Young’s double slit experiment is replaced by a monochromatic blue light of the same intensity [1992]
As 
∴ Fringe width β will decrease
Interference was observed in interferencechamber where air was present, now the chamberis evacuated, and if the same light is used, acareful observer will see [1993]
In vaccum, λ increases very slightly compared to that in air. As β∝ λ , therefore, width of interference fringe increases slightly.
A parallel beam of monochromatic light ofwavelength 5000Å is incident normally on asingle narrow slit of width 0.001 mm. The light isfocussed by a convex lens on a screen placed infocal plane. The first minimum will be formed forthe angle of diffraction equal to [1993]
For first minimum, a sin θ = nλ = 1λ
In a Fresnel biprism experiment, the two positionsof lens give separation between the slits as 16cm and 9 cm respectively. What is the actualdistance of separation? [1996]
Separation between slits are (r1=) 16 cm and (r2=) 9 cm.
Actual distance of separation
Colours appear on a thin soap film and on soapbubbles due to the phenomenon of [1999]
We know that the colours for which the
condition of constructive interference is
satisfied are observed in a given region of the film. The path difference between the light waves reaching the eye changes when the position of the eye is changed. Therefore, colours appear on a thin soap film or soap bubbles due to the phenomenon of interference.
Which of the following shows particle nature oflight? [2001]
Photoelectric effect shows particle nature of light as light consists of packets of energy called photons or quanta
A paper, with two marks having separation d, isheld normal to the line of sight of an observer ata distance of 50m. The diameter of the eye-lensof the observer is 2 mm. Which of the followingis the least value of d, so that the marks can beseen as separate ? The mean wavelength ofvisible light may be taken as 5000 Å. [2002]
The periodic waves of intensities I1 and I2 pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:
We know that the resultant of two intensities with phase difference of angle a can be represented as, I = I1+ I2 + 2( I1.I2 )1/2. cos a
Thus we get Imax = I1+ I2 + 2( I1.I2 )½
And Imin = I1+ I2 - 2( I1.I2 )½
Thus we get the sum = 2( I1+ I2 )
A lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter
2/d in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be
respectively:
By covering aperture, focal length does not change. But intensity is reduced by 1/4 times, as aperture diameter d/2 is covered.
∴ New focal length = f and intensity = 3I/4
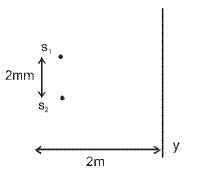
In Young’s double slit experiment, the slits are 2 mmapart and are illuminated by photons of twowavelengths λ1 = 12000Å and λ2 = 10000Å. Atwhat minimum distance from the common centralbright fringe on the screen 2 m from the slit will abright fringe from one interference patterncoincide with a bright fringe from the other ? [NEET 2013]
∴ n1 λ1 = n2λ2
⇒ n1 × 12000 × 10–10 = n2 × 10000 × 10–10
or, n (12000 × 10–10) = (n + 1) (10000 × 10–10)
⇒n = 5
(∵ λ1 = 1200 x 10-10m; λ2 = 10000 x 10-10m)
(∵ d = 2 mm and D = 2m)
= 5 × 12 × 10–4 m
= 60 × 10–4 m
= 6 × 10–3m = 6 mm
A parallel beam of fast moving electrons isincident normally on a narrow slit. A fluorescentscreen is placed at a large distance from the slit.If the speed of the electrons is increased, whichof the following statements is correct ? [NEET 2013]
Angular width, 
[For central maxima n = 1]
Hence, with increase in speed of
electrons angular width of central
maximum decreases.
In Young’s double slit experiment the distancebetween the slits and the screen is doubled. Theseparation between the slits is reduced to half.As a result the fringe width [NEET Kar. 2013]
Fringe width 
From question D' = 2D and d' = d/2
A parallel beam of light of wavelength λ is incident normally on a narrow slit. A diffraction pattern is formed on a screen placed perpendicular to the direction of the incident beam. At the second minimum of the diffraction pattern, the phase difference between the rays coming from the two edges of slit is [NEET Kar. 2013]
Conditions for diffraction minima are
Path diff. Δx = nλ and Phase diff. δφ = 2nπ
Path diff. = nλ = 2λ
Phase diff. = 2nπ = 4π (∵n = 2)
|
157 videos|452 docs|213 tests
|
|
157 videos|452 docs|213 tests
|
How to Prepare for NEET
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
