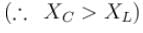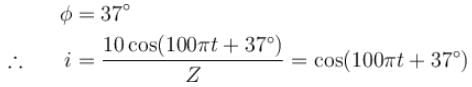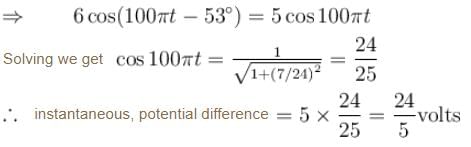Alternating Current NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Alternating Current NAT Level - 2
In an AC circuit the potential differences across an inductance and resistance joined in series are respectively 16V and 20V. The total potential difference across the circuit is X/5. Then X is :
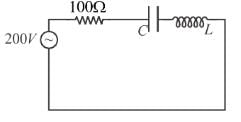
A LCR series circuit with 100Ω resistance is connected to an AC source of 200V and angular frequency 300 radians per second. When only the capacitance is removed, the current lags behind the voltage by 60°. When only the inductance is removed, the current leads the voltage by 60°. Calculate the average power dissipated in LCR circuit in watts.
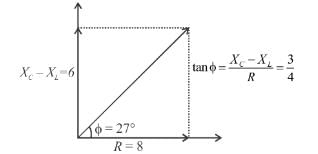
An inductor (XL = 2Ω) a capacitor (XC = 8Ω) and a resistance 8Ω are connected in series with an AC source. The voltage output of AC source is given by V = cos100πt, then the impedance of the circuit (in Ω).

A LCR series, AC circuit operates at half its resonant frequency and at a power factor of 0.8. Then the ratio of 
In the LCR circuit shown if only L is removed, the current leads the supply voltage by 30°. If only C is removed the current lags the voltage by 60°. The resonant frequency is 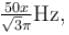 then what is the value of x.
then what is the value of x.
The voltage time (V-t) graph for triangular wave having peak value V0 is as shown in figure. The rms value of V in time interval from t = 0 to T/4 is  Then, X is :
Then, X is :

The average value of current i = Im sin ωt from t = π/2ω to t = 3π/2ω is how many times of Im ?
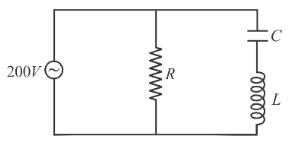
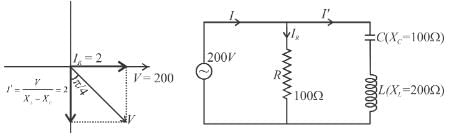
In the circuit diagram shown, XC = 100Ω, XL = 200Ω and R = 100Ω. The effective current through the source is √N. Then N is :
Find the average value of current from t = 0 to t = 2π/ω, if the current varies as i = Imsinωt.
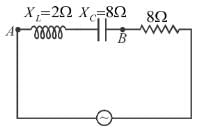
An inductor (XL = 2Ω), a capacitor (XC = 8Ω) and a resistance 8Ω are connected in series with an AC source. The instantaneous potential difference between A and B when it is half of the voltage output from source at that instant is x/5 volt, then x is.


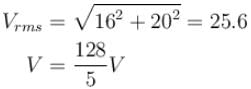
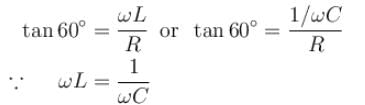
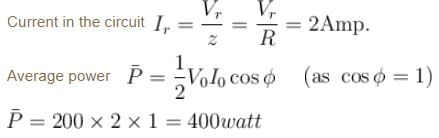

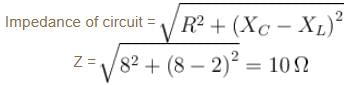
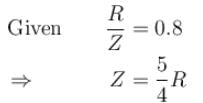

 resonant frequency
resonant frequency 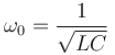
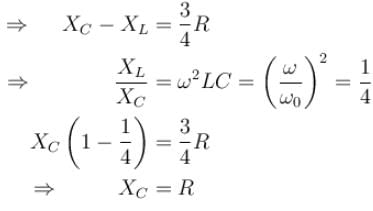
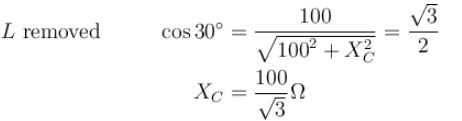
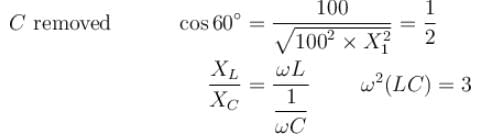
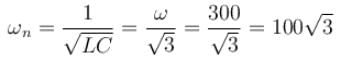

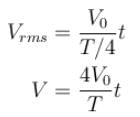
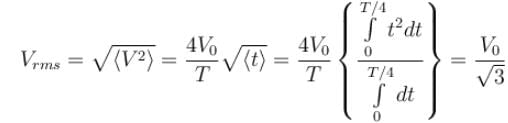

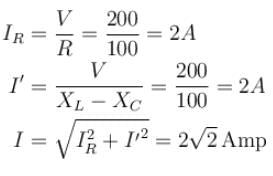
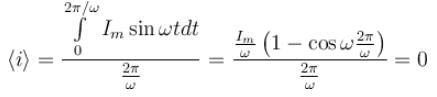
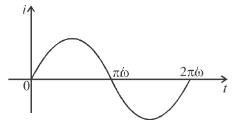
 is one cycle.
is one cycle.