Analytical Reasoning Quiz I, Non Verbal Reasoning - Bank Exams MCQ
15 Questions MCQ Test Reasoning Aptitude for Competitive Examinations - Analytical Reasoning Quiz I, Non Verbal Reasoning
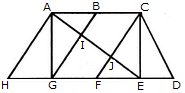
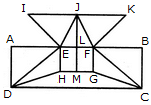
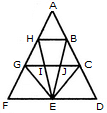
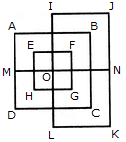
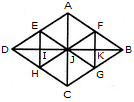
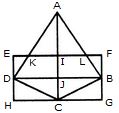
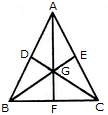
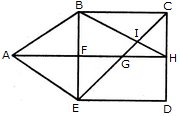
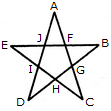
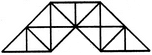
Find the number of triangles in the given figure.
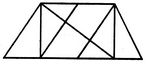

Find the minimum number of straight lines required to make the given figure.
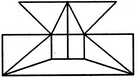

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
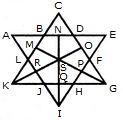
Find the number of triangles in the given figure.
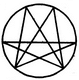

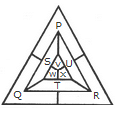
Find the number of triangles in the given figure.
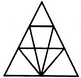
Find the minimum number of straight lines required to make the given figure.
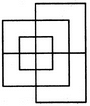
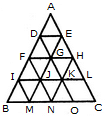
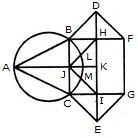
Find the number of triangles in the given figure.
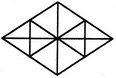
Find the number of triangles in the given figure.
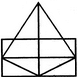
Find the number of triangles in the given figure.
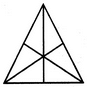
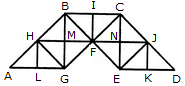
Find the number of triangles in the given figure.
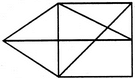
Find the number of triangles in the given figure.
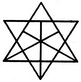
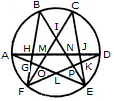
What is the minimum number of colours required to fill the spaces in the given diagram without any two adjacent spaces having the same colour?
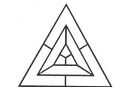
Find the minimum number of straight lines required to make the given figure.
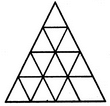
Find the number of triangles in the given figure.

Find the number of triangles in the given figure.
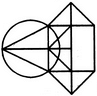
Find the number of triangles in the given figure.
|
11 videos|20 docs|171 tests
|
|
11 videos|20 docs|171 tests
|