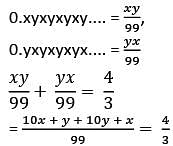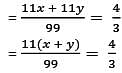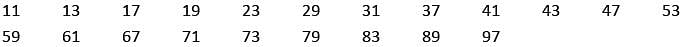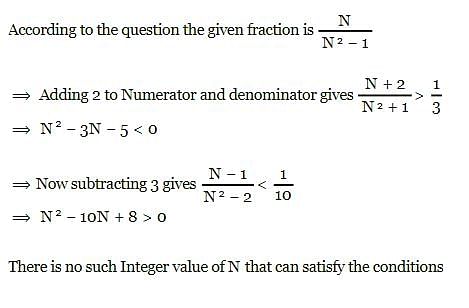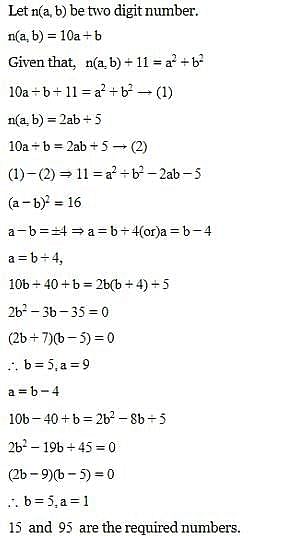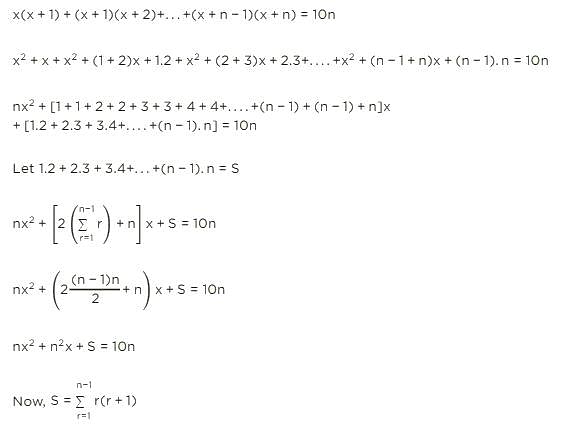Arun Sharma Test: Number System- 3 - Interview Preparation MCQ
20 Questions MCQ Test Quantitative Aptitude (Quant) - Arun Sharma Test: Number System- 3
0.xyxyxyxy.... + 0.yxyxyxyx = 4/3, if x and y are natural numbers what would be the value of x + y?
The sum of first five, 3 digit prime numbers is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a, (a+2), (a+4) are all prime numbers, how many such values can 'a' take?
What is the sum of all the negative two digit prime numbers?
What is the negative of sum of all the two digit prime numbers?
For the equation (2a + 3b + 9c) to be even, we must have
What is the difference between the highest and smallest 3 digit prime number?
Suppose the sum of n consecutive integers is x+(x+1) +(x+2) +(x+3)+...+(x+(n-1)) =1000, then which of the following cannot be true about the number of terms n?
What would the remainder when the square of the largest 4 digit prime number is divided by 6?
Let us consider a fraction whose denominator is smaller than the square of the numerator by unity. If we add 2 to the numerator and the denominator, the fraction will exceed1/3; now if we subtract 3 from the numerator and the denominator, the fraction remains positive but smaller than 1/10. Find the fraction.
If we divide a two-digit number by the sum of its digits, we get 4 as a quotient and 3 as a remainder. Now if we divide that two-digit number by the product of its digits, we get 3 as a quotient and 5 as a remainder and the two-digit number.
What two-digit number is less than the sum of the squares of its digits by 11 and exceed their doubled product by 5?
The last three - digits of the multiplication 12345 × 54321 will be
Find the gcd (111....11 hundred ones; 11....11 sixty ones).
The remainder when 1010+10100+101000+....+1010000000000 is divided by 7 is
What is the maximum number of elements that one can pick from the set of natural numbers from 1 to 20 such that the product of no two of them results in a perfect square or perfect cube?
For a positive integer n, the quadratic equation x(x+1)+(x+1)(x+2)+......+(x+n−1)(x+n)=10 n has two consecutive integral solutions, then n is equal to.
The remainder when 22 +222 +2222 +22222 +..... (222..... 49 twos)2 is divided by 9 is
Twenty five sets of problems on Data Interpretation one each for the DI sections of 25 CATALYST tests were prepared by the AMS research team. The DI section of each CATALYST contained 50 questions of which exactly 35 questions were unique, i.e. they had not been used in the DI section of any of the other 24 CATALYSTS. What could be the maximum possible number of questions prepared for the DI sections of all the 25 CATALYSTS. What could be the maximum possible number of questions prepared for the DI sections of all the 25 CATALYSTS put together?
The least number, which is to be added to the greatest number of 4 digits so that the sum may be divisible by 345, is
|
164 videos|139 docs|118 tests
|
|
164 videos|139 docs|118 tests
|