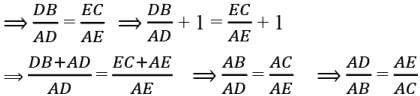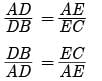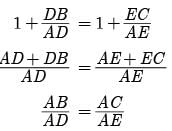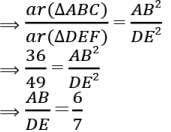EduRev

Get the App Signup / Login

Welcome Back

Forgot Password?

New User? Sign Up

Create your account now

I accept the Terms & Conditions.

Already Have an Account? Login

Assertion & Reason Test: Triangles - 2

10 Questions MCQ Test Online MCQ Tests for Class 10 | Assertion & Reason Test: Triangles - 2

Description

Attempt Assertion & Reason Test: Triangles - 2 | 10 questions in 20 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study Online MCQ Tests for Class 10 for Class 10 Exam | Download free PDF with solutions

QUESTION: 1

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Two similar triangle are always congruent.
Reason : If the areas of two similar triangles are equal then the triangles are congruent.

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

Solution: Two similar triangles are not congruent generally.

So, A is incorrect but R is correct.

QUESTION: 2

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : ABC is an isosceles triangle right angled at C then AB² = 2AC².
Reason : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

Solution: We know that If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. This is converse of Pythagoras theorem.

So, Reason is correct By

Pythagoras theorem, we have AB² = AC² + BC²

= AC² + AC² [∵ AC = BC Given]

⇒ AB² = 2AC²

So, Assertion is also correct.

But reason (R) is not the correct explanation of assertion (A).

QUESTION: 3

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : ΔABC is an isosceles triangle right angled of C , then AB² = 2AC².
Reason : In right ΔABC , right angled at B, AC² =AB² +BC².

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

Solution: In an isosceles ΔABC , right angled at C is

AB² = AC² + BC²

AB² = AC² + AC²

AB² = 2AC² (AC = BC)

So, both A and R are correct and R explains A.

QUESTION: 4

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : ABC is an isosceles triangle with AC = BC. If AB² = 2 AC², then ΔABC is a right triangle.

Reason : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

So, Reason is correct

AB² = 2AC² = AC² + AC²

= BC² + AC² [∵ AC = BC Given]

⇒ AB² = BC² + AC²

By converse of Pythagoras theorem, ΔABC is a right angled triangle.

So, Assertion is also correct.

QUESTION: 5

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : ΔABC ~ ΔDEF such that ar(ΔABC) = 36cm² and ar(ΔDEF) = 49cm² then, AB : DE = 6 :7

Reason : If ΔABC ~ ΔDEF , then ar(ΔABC)/ar(ΔDEF) = AB²/DE² = BC²/EF² = AC²/DF²

A.
Both A and R are true and R is the correct explanation of A
B.
Both A and R are true but R is NOT the correct explanation of A
C.
A is true but R is false
D.
A is false and R is True

Solution:

ar(ΔABC)/ar(ΔDEF) = AB²/DE²

36/49 = AB²/DE²

AB/DE = 6/7

AB:DE = 6:7

So, both A and R are correct and R explain A.

QUESTION: 6

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : In the ∆ABC , AB = 24 cm, BC = 7 cm and AC = 25 cm, then ∆ABC is a right angle triangle.

Reason : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

Solution: We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

So, Reason is correct

Now, AB² + BC² = 24² + 10²

= 576 + 49 = 625

= AC²

⇒ AB² + BC² = AC²

By converse of Pythagoras theorem, ∆ABC is a right angled triangle.

So, Assertion is also correct.

But reason (R) is not the correct explanation of assertion (A).

QUESTION: 7

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

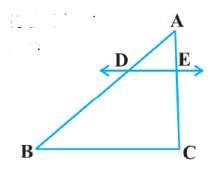
Assertion : In ∆ABC , DE|| BC such that AD = (7x - 4)cm, AE = (5 - 2)cm, DB = (3 + 4) cm and EC = 3 cm than x equal to 5.

Reason : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distant point, than the other two sides are divided in the same ratio.

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

Solution: We have,

AD/DB = AE/EC

21x² - 12x = 15x² + 20x - 6x - 8x

6x² - 26x + 8 = 0

3x² - 13x + 4 = 0

3x² - 12x - x + 4 = 0

3x(x - 4) - 1(x - 4) = 0

(x - 4) (3x - 1) = 0

So, A is incorrect but R is correct.

QUESTION: 8

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

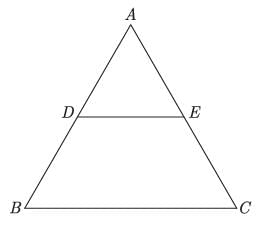
Assertion : If a line intersects sides AB and AC of a Δ ABC at D and E respectively and is parallel to BC, then AD/AB = AE/AC

Reason : If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio.

A. Both A and R are true and R is the correct explanation of A
B. Both A and R are true but R is NOT the correct explanation of A
C. A is true but R is false
D. A is false and R is True

Solution: We know that If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio. This is Basic Proportionality theorem.

So, Reason is correct.

By Basic Proportionality theorem, we have AD/DB = AE/EC

So, Assertion is correct

QUESTION: 9

Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion : Assertion : If in a ∆ABC , a line DE || BC , intersects AB in D and AC in E , then AB/AD = AC/AE

Reason : If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.