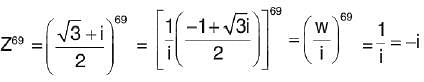BITSAT Mathematics Test - 7 - JEE MCQ
30 Questions MCQ Test - BITSAT Mathematics Test - 7
Interval of λ for which both roots of the equation 3x2 + (2λ +1)x + 3λ2 = 0 lie in the interval (0,3), is
If the roots of equation (x−b)(x−c)+(x−c)(x−a)+(x−a)(x−b)=0 are equal, then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the roots of the equation (b−c)x2+(c−a)x+(a−b)=0 be equal then a, b, c are in
If α, β be the roots of x2+px+q=0 and α+h, β+h are the roots of x2+rx+s=0 then-
Let p,q and r be real numbers (p≠q,r≠0, such that the roots of the equation 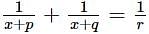 are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to
are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to
If α+β=−2 and α3+β3=−56, then the quadratic equation whose roots are α and β is
If λ be the ratio of the roots of the quadratic equation in x, 3m2x2+m(m−4)x+2=0, then the least value of m for which is
is
The set of values of a for which 1 1 lies between the roots of equation x2−ax−a+3=0 is
Let G={(b,b),(b,c),(c,c),(c,d)} and H={(b,a),(c,b),(d,c)}. Then the number of elements in the set (G∪H)⊕(G∪H)−1, where ⊕ denotes the symmetric difference, is
For real numbers x and y, we write xRy ⟺ x−y+√2 is an irrational number. Then the relation R is.
Let R1 and R2 be two relations defined as follows : R1={(a, b)∈R2:a2+b2∈Q} and R2={(a, b)∈R2:a2+b2∉Q}, where Q is the set of all rational numbers, then
The relation R defined on the set of natural numbers as (a,b):a differs from b by 3 is given as
If we define a relation R on the set N×N as (a,b) R (c,d)⇔a+d=b+ c for all (a,b),(c,d)∈N×N, then the relation is
If a set A has 5 elements, then the number of ways of selecting two subsets P and Q from A such that P and Q are mutually disjoint, is
Let X={x:x is a multiple of 3} 3 } and Y={x:x is a multiple of 5}. 5 } . Then X−Y is equal to
Set A contains n elements and is defined as A={1,2,3,.....n}. Then the number of subsets of A having at least one odd integer must be ([.] denotes greatest integer ≤ x)
For any two sets A and B , the values of [(A−B)∪B]C is equal to
The value of c , in the Lagrange’s mean value theorem for the function f(x)=x3−4x2+8x+11, when x∈[0,1] is
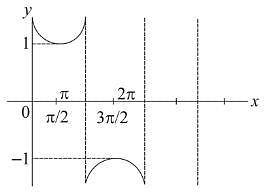
The function which is neither decreasing nor increasing in 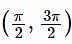 is
is
The volume V and depth x of water in a vessel are connected by the relation 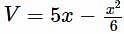 and the volume of water is increasing at the rate of 5 cm3/sec. When x = 2 cm, the rate at which the depth of water is increasing is
and the volume of water is increasing at the rate of 5 cm3/sec. When x = 2 cm, the rate at which the depth of water is increasing is
The number of points in (−∞,∞) for which x2−xsinx−cosx=0, is:
A polynomial given by the equation 4ax3 +3bx2+2cx+d=0 satisfy the condition 27a+9b+3c=0,then it has at least one real root lying in the interval
The normal to the curve x=a(1+cosθ), y=asinθ always passes through the fixed point
If z is a complex number, then I3z - 11 = 3 Iz - 2I represents
What is the remainder obtained by dividing kx2 + x - 1 by x + 2k ?


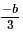 <3, D≥0
<3, D≥0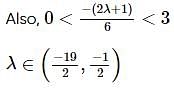
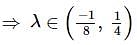
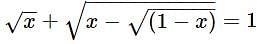 is
is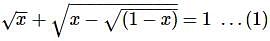
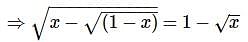
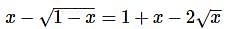
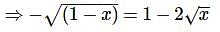
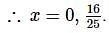
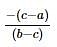
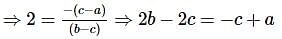
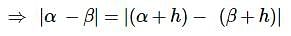
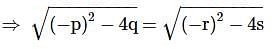
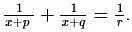
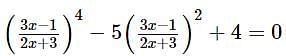 are
are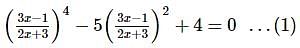
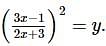 The equation (1) becomes
The equation (1) becomes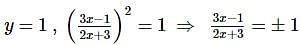
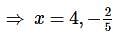
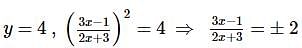
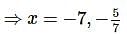
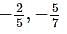
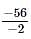 - 28 [α + β = -2]
- 28 [α + β = -2]
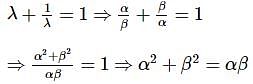
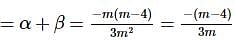
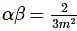

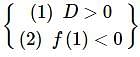
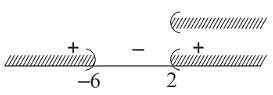
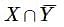 ={0,3,6,9,12,15,18,....}∩{1,2,3,4,6,7,8,9,....}
={0,3,6,9,12,15,18,....}∩{1,2,3,4,6,7,8,9,....}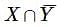
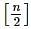
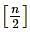
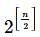
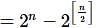
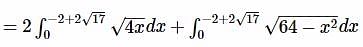
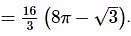
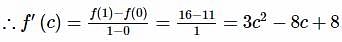
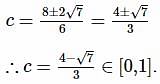
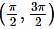
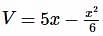
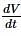 is the rate at which volume of water is increasing.
is the rate at which volume of water is increasing.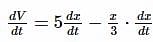
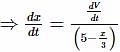
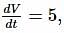 when x = 2
when x = 2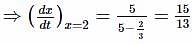 cm/sec.
cm/sec.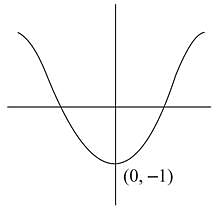
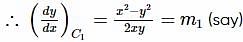
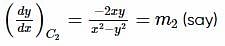
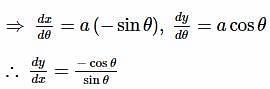
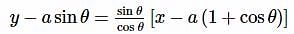
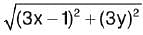 = 9x2 + 9y2 - 36 x
= 9x2 + 9y2 - 36 x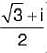 then z69 is equal to
then z69 is equal to