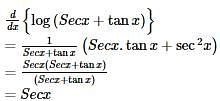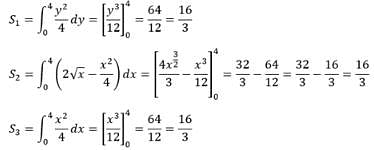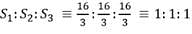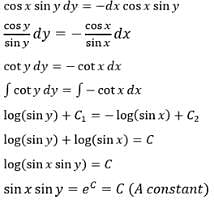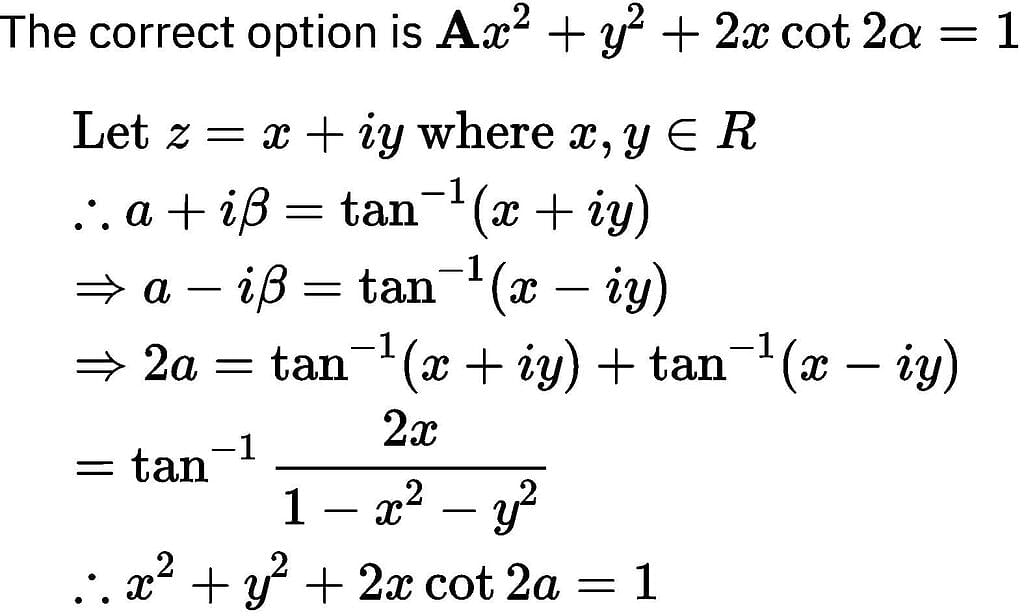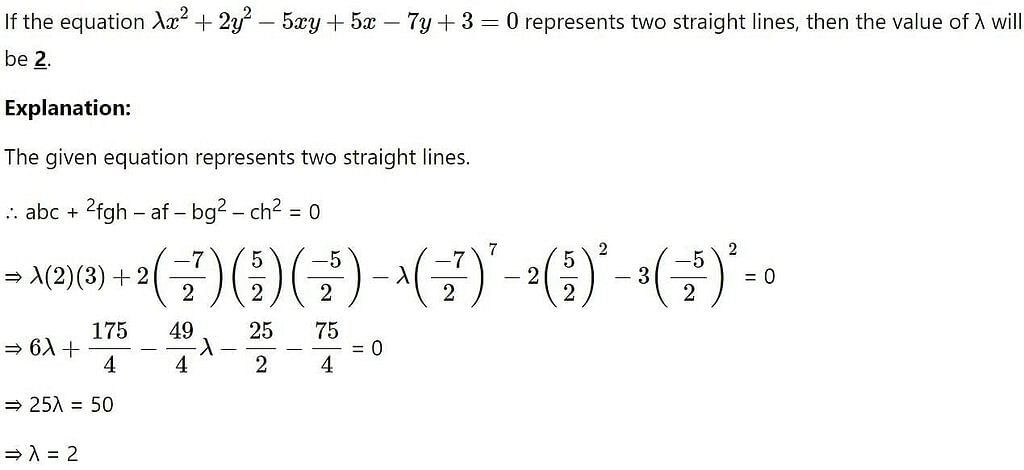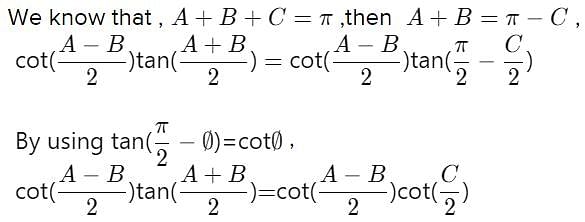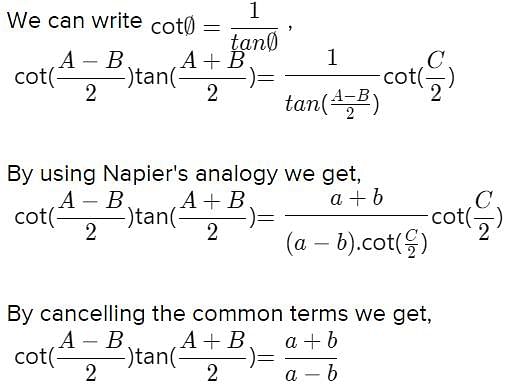BITSAT Maths Test - 1 - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - BITSAT Maths Test - 1
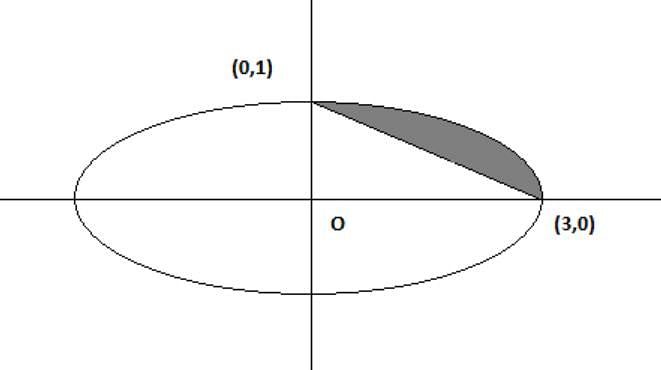
The area enclosed between the ellipse x2 + 9y2 = 9 and the straight line x + 3y = 3, in the first quadrant is
The coefficient of x-9 in the expansion of ((x2/2) - (2/x))9 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The differential equation of the family of lines through the origin is
The circles x2 + y2 - 12x -12y = 0 and x2 + y2 + 6x + 6y = 0
Length of tangent drawn from (5,1) to the circle x2 + y2 + 6x - 4y - 3 = 0 is
The solution of differential equation (dy/dx) = [(x(2logx + 1)) / (siny + ycosy)] is
In an Argand plane the inequality π/4 < arg (z) < π/3 represent the region bounded by
The product of the perpendicular, drawn from any point on a hyperbola to its asymptotes is
From the top of the house 15 metres high the angle of depression of a point which is at a distance 15 m from the base of the house is
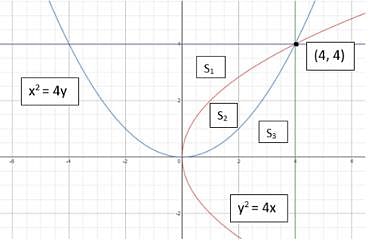
The parabolas y2 = 4x and x2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes. If S₁, S₂, S₃ are respectively the areas of these parts numbered from top to bottom; then S₁ : S₂ : S₃ is
The solution of the differential equation cos x sin y dx + sin x cos y dy = 0 is
A and B are square matrices of order n x n, then (A - B)2 is equal to
If α + i β = tan⁻1 z, z = x + yi and α is constant, then locus of \'z\' is
If equation λx2 + 2y2 - 5xy + 5x - 7y + 3 = 0, represents two straight lines, the value of λ is
The locus of the point of intersection of two normals to the parabola x2=8y, which are at right angles to each other,is
The equation of the parabola with its vertex at (1,1) and focus at (3,1) is
Out of 6 boys and 4 girls a group of 7 is to be formed. In how many ways can this be done if the group is to have a majority of boys?
How many even numbers can be formed by using all the digits 2, 3, 4, 5, 6?
A committee of five is to be chosen from a group of 9 people. The probability that a certain married couple will either serve together or not at all is
A six-faced dice is so biased that it is twice as likely to show an even number as an odd number when thrown. It is thrown twice. The probability that the sum of two numbers thrown is even is
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|


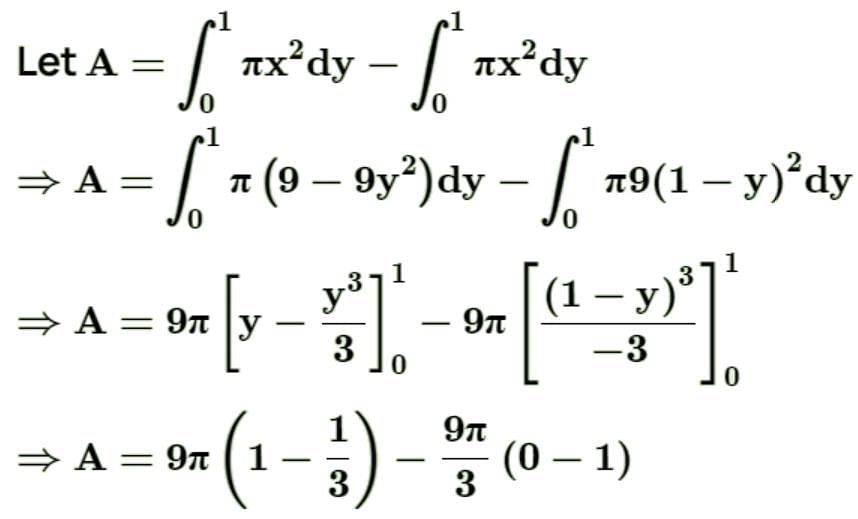
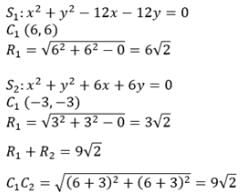
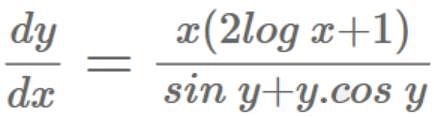
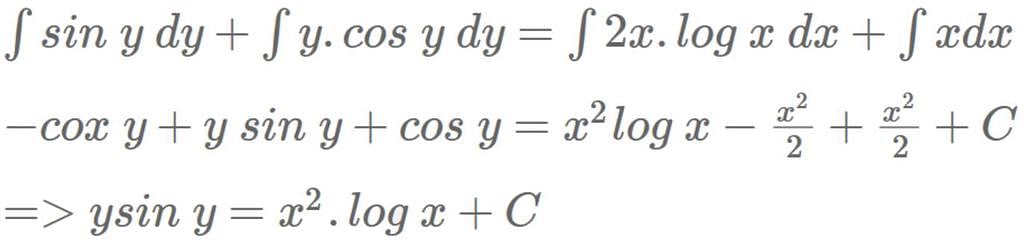
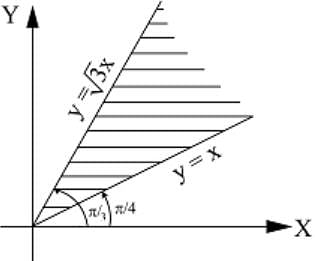
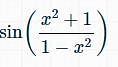 , find dy/dx
, find dy/dx