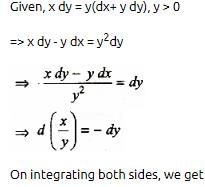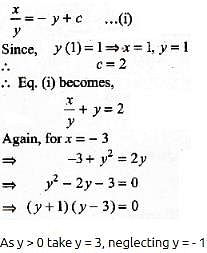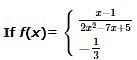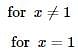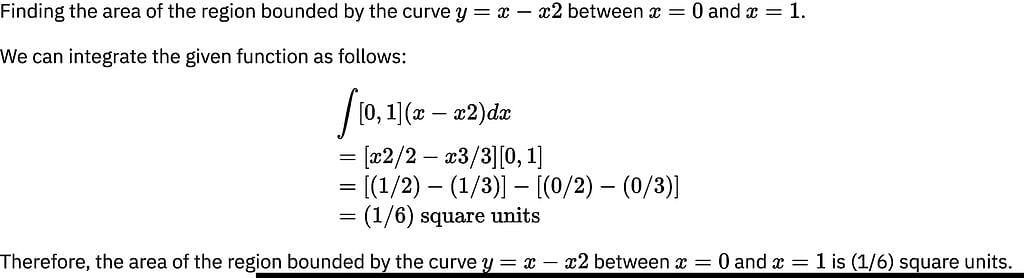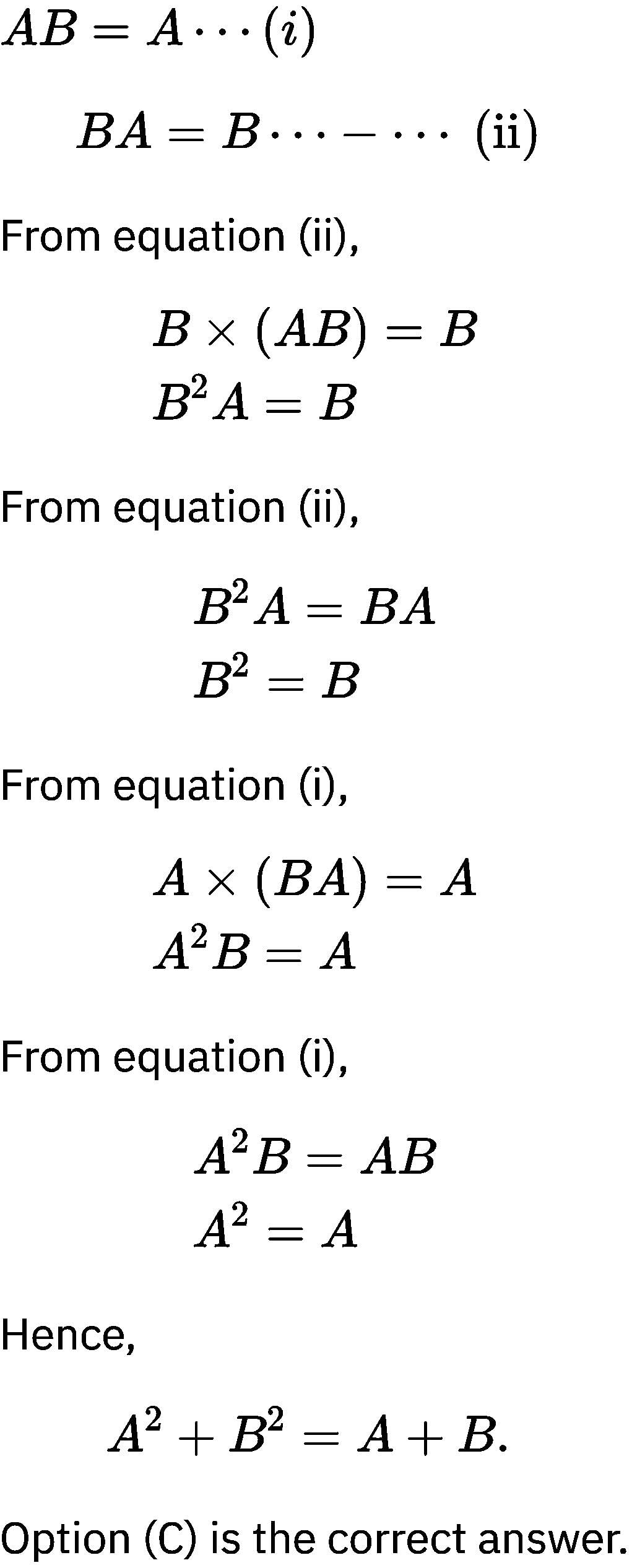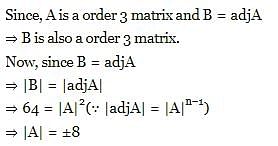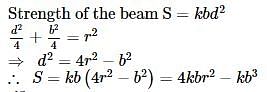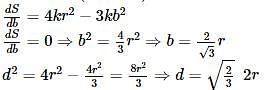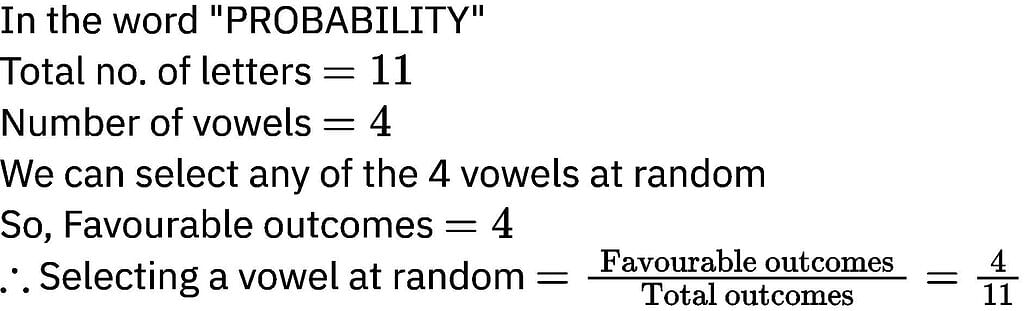BITSAT Maths Test - 2 - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - BITSAT Maths Test - 2
The area (in square units) of the region enclosed by the curves y = x2 and y = x3 is
In the expansion of (y1/6 - y-1/3)9 the term independent of y is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the two circles 2x2 + 2y2 -3x + 6y + k = 0 and x2 + y2 - 4x + 10y + 16 = 0 cut orthogonally, then the value of k is
Equation of the diameter of the circle x2 + y2 - 6x + 2y = 0 which passes thro' the origin is
The order and degree of differential equation √(dy/dx) - 4 (dy/ dx) - 7x = 0 are
If x dy = y(dx + y dy), y > 0 and y (1) = 1, then y (-3) is equal to
The length of the shadow of a rod inclined at 10o to the vertical towards the sun is 2.05 metres when the elevation of the sun is 38o.The length of the rod is
The product of the perpendicular, drawn from any point on a hyperbola to its asymptotes is
The area of the region bounded by the curve y = x - x2 between x = 0 and x = 1 is
The area bounded by the curve x = at2, y = 2at and the X-axis is 1 ≤ t ≤ 3 is
The sum of first 50 terms of the series cot⁻13 + cot⁻1 7 + cot⁻1 13 + cot⁻1 21 + ... is
If A and B are two matrices such that AB = B and BA = A, then A2 + B2 is equal to
if A is a 3 x 3 matrix and B is its adjoint matrix. If ∣B∣ = 64, then ∣A∣ =
The strength of a beam varies as the product of its breadth b and square of its depth d. A beam cut out of a circular log of radius r would be strong when
Equation 2x2+7xy+3y2+8x+14y+λ=0 represents a pair of straight lines, value of λ is
How many total words can be formed from the letters of the word INSURANCE in which vowels are always together?
A single letter is selected at random from the word "PROBABILITY". The probability that it is a vowel is
A committee consists of 9 experts from three institutions A, B and C, of which 2 are from A, 3 from B and 4 from C. If three experts resign, then the probability that they belong to different institutions is
If the area of a Δ A B C be λ then a2 sin 2B + b2 sin 2A is equal to
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|




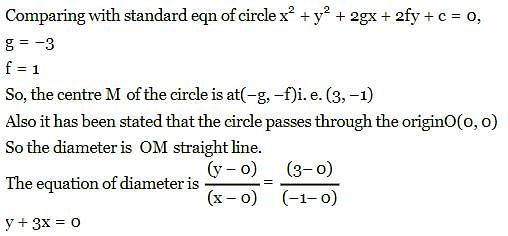
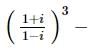
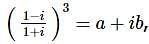 then a and b are
then a and b are