BITSAT Mock Test - 4 - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - BITSAT Mock Test - 4
Bullets of mass 0.03 kg each hit a plate at the rate of 200 bullets per second with a velocity of 50 ms-1 and reflect back with a velocity of 30 ms-1. The average force (in Newton) acting on the plate is
A train blowing its whistle moves with a constant velocity u away from an observer on the ground. The ratio of the actual frequency of the whistle to that measured by the observer is found to be 1.2. If the train is at rest and the observer moves away from it at the same velocity, then the ratio would be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In an inductor, the current I (in amperes) varies with time t (in seconds) as I = 5 + 16t. If the emf induced in the inductor is 10 mV, then the power supplied to the inductor at t = 1 s is
Blocks A and B of masses 2m and m are connected as shown in the figure. The spring has negligible mass. The string is suddenly cut. The respective magnitudes of acceleration of masses 2m and m at that instant are
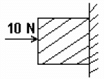
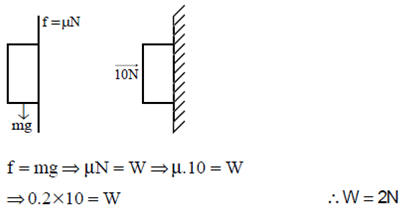
A horizontal force of 10 N is necessary to just hold a stationary block against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
The flux linked with a coil at any instant t is given by
φ = 10t2 - 50t + 250
The induced emf at t = 3 s is
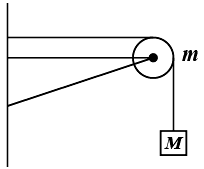
A string of negligible mass, going over a clamped pulley of mass m, supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by
A block of mass m is lying on another block of mass M, lying on a horizontal frictionless surface as shown in the figure. The coefficient of static friction between the two blocks is 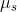 . If a force F (>
. If a force F (> 

 - particle (mass 4m and charge +2e) so that it revolves in a circular orbit of the same radius in the same magnetic field?
- particle (mass 4m and charge +2e) so that it revolves in a circular orbit of the same radius in the same magnetic field?
A uniform rope of length 12 m and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced in the lower end of the rope. What is the wavelength of the pulse, when it reaches the top of the rope?
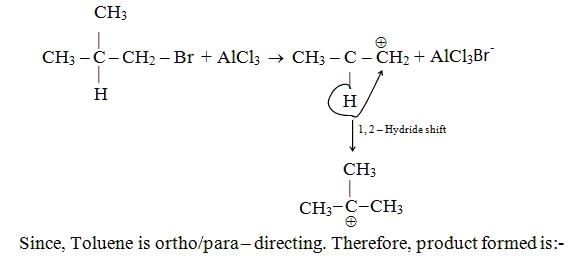
At a certain temperature, the vapour pressures of benzene and toluene are 119 torr and 37 torr, respectively. The mole fraction of toluene in the vapour phase, which is in equilibrium with a solution of benzene and toluene in 1 : 1 molar ratio, is




Which of the following represents the correct order of decreasing number of S=O bonds?
Directions: In this question, Problem figures 1 and 2 are related in some way. Similarly, Problem figures 3 and 4 are related, but Problem figure 4 is missing. Find out the correct alternative from the given options for that.

Directions: In the following question, a number series is given with one term missing. Choose the correct alternative that will continue the same pattern and replace the question mark in the given series.
3, 4, 7, 14, 4, 5, 9, 18, 5, 6, 11, ?
The coefficient of variation of two samples is 2.5 and 3 and their mean is 40 and 50, respectively. What is the difference in variances?
The number of common tangents to the circles x2 + y2 + 2x + 8y − 25 = 0 and x2 + y2 − 4x − 10y + 19 = 0 is
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|


 ...(i)
...(i)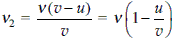
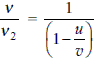 ...(ii)
...(ii)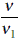 = 1 +
= 1 + 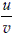 or 1.2 = 1 +
or 1.2 = 1 + 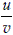 , or u = 0.2 v or
, or u = 0.2 v or 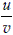 = 0.2.
= 0.2.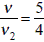 = 1.25.
= 1.25.


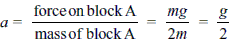


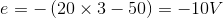

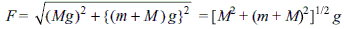 which is choice (4).
which is choice (4).
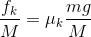
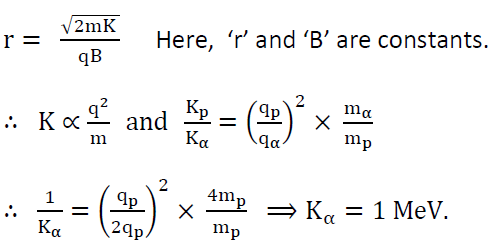

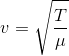
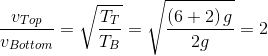
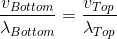
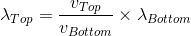
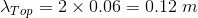
 = 0.5
= 0.5  37 torr = 18.5 torr
37 torr = 18.5 torr = Ptoluene/Ptotal = 18.5/78.0 = 0.237
= Ptoluene/Ptotal = 18.5/78.0 = 0.237 , at equilibrium
, at equilibrium 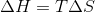


 = 30,560 J mol-1
= 30,560 J mol-1



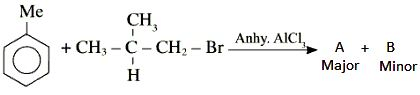



 is equal to
is equal to

 {cos(π - x) = cos(π + x) = -cos x
{cos(π - x) = cos(π + x) = -cos x
 0 ≤ cos-1 x ≤ π)
0 ≤ cos-1 x ≤ π)


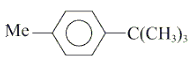
 , Where x ≠ -5, then f-1(x) is equal to
, Where x ≠ -5, then f-1(x) is equal to
 , where
, where 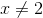 .
. ,
, are any two vectors, then |
are any two vectors, then |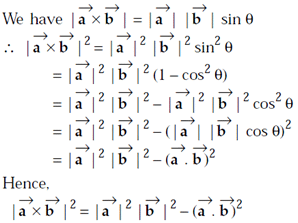
 is equal to
is equal to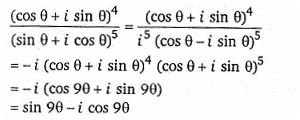
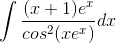 is equal to
is equal to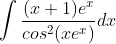
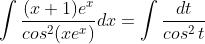
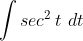
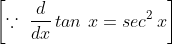
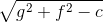 =
= 

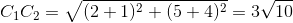
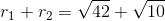
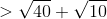
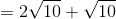
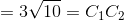


 It means circles intersecting each other.
It means circles intersecting each other.
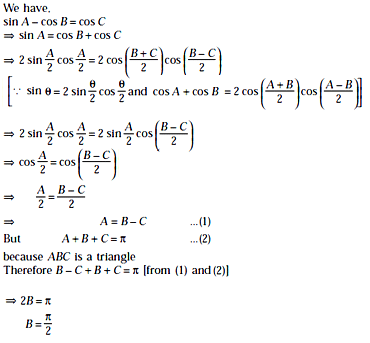
 equals
equals














