Business Mathematics Mock Test - 2
100 Questions MCQ Test Mock Tests & Past Year Papers for CA Foundation | Business Mathematics Mock Test - 2
| 1 Crore+ students have signed up on EduRev. Have you? |
An object of a set is called an element.
Elements of a set are represented within curly braces{}.
If R is a relation from a finite set A having m elements to a finite set B having n elements, then the number of relations from A to B is
First term of the AP, a=21
Common difference d=21
nth term is 210
Then,
210=a+(n−1)d
210=21+(n−1)×21
210=21n
Therefore, n=10
Hence, 210 is 10th term of the series.
Given,
f(x)=3x−7
Putting 2 in place of x, we get
f(2)=3×2−7
f(2)=6−7=−1
The reciprocal ratio of a:b is b:a
∴ reciprocal ratio of 121x3: 25x3 is 25x3:121x3
If the relation R:A→B, where A={1,2,3} and B={1,3,5} is defined by R={(x,y):x<y,x∈A,y∈B}, then
The number of permutations of four letter words obtained from the letters of the word "ARTICLE"is
ARTICLE - total letters : 7
out of them four letters should be
selected to be permutated
= 7P4
Option : D
Replace the ? with appropriate alphabet group to complete the given series.
DFST, FSTD, STDF, ?
The first letter in each group is the last letter in the next group, i.e
STDF→TDFS
Hence,option C is the correct answer.
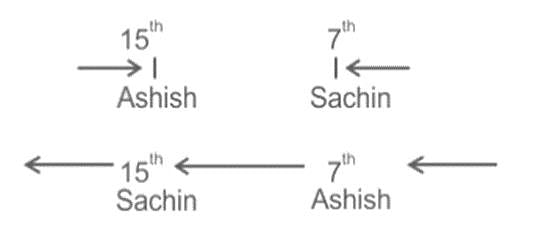
Student line up in a queue in which Ashish stands fifteenth from the left and Sachin is seventh from the right. If they interchange their places, Sachin would be fifteenth from the right. How many students are there in the queue?
Sachin's new position if 15th from the right as well as left.
Hence, number of students in the queue
=14+1=14
=29
Hence the answer is option C
Find two numbers such that twice of the first added to the second gives 21, and twice the second added to the first gives 27.
Let the first number is x and second is y
Given twice of first added with second gives 21
∴2x+y=21 ...(1)
And given twice of second added with first gives 27
∴x+2y=27 ...(2)
Multiply (1) by 2
Then 4x+2y=42 ...(3)
Subtract (3) with (2)
Then 3x=15
Or x=5
Put the value of x=5 in (1)
Then 10+y=21
Or y=21−10
Or y=11
Then first number is 5 and second is 11.
Let A={a,b,c} and B={4,5} Consider a relation R defined from set A to set B then R is subset of
If A and B are two non empty sets, the relation from set A to set B is denoted as A×B
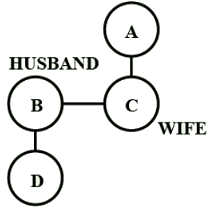
If P+Q means P is husband of Q, P/Q means P is sister of Q, P∗ Q means P is the son of Q. How is D related to A in D∗B+C/A?
P+Q means P is husband of Q
P/Q means P is sister of Q
P∗ Q means P is the son of Q
D∗B means D is the son of B
C/A means C is sister of A
B+C means B is husband of C
So, D is nephew of A.
Hence, Option B is correct.
Find the ratio of the following :
Q. The speed of cycle is 15km per hour to the speed of scooter 30km per hour.
Speed of cycle which is 15km/hr to the speed of scooter which is 30km/hr=15km/30km=1/2=1:2
If in a certain language 'mu mit es' means 'who is she' and 'elb mu es' means 'where is she', then what is the code for 'where' in this language?
Neelam, who is Deepak's daughter, says to Deepika, "Your mother Rekha is the younger sister of my father who is the third child of Ramlal." How is Ramlal related to Deepika?
Neelam's father is Deepak.
Deepika's mother is Rekha.
Deepak is the third child of Ramlal.
So, Deepak's younger sister Rekha is the daughter of Ramlal.
So, Ramlal is the father of Rekha and the grandfather of her daughter Deepika.
option C.
The reciprocal ratio of a:ba:b is b:ab:a
∴ reciprocal ratio of 81:121 is 121:81.
What is the first four terms of the A.P. whose first term is 3 and common difference is 5?
Here the set A={a,b,c} has finite number of elements. Hence set A is a finite set.
. Choose the correct option.
The sum of the present ages of father and his son is 60 years. 6 years ago, father age was five times the age of the son. After six years son's age will be
Let father's age =F
son's age =S
then F+S=60...(1)
and, F−6=5(S−6)
F=5S−24...(2)
From (1),F=60−S
Thus, 60−S=5S−24
84=6S
S=14 years
Present age of son is 14 years.
Hence, after 6 years, son will be 20 years of age
In how many ways can we select 5 people from a group of 9 people so that a particular person is never to be included
Out of 9 people, one has not to be selected.
Therefore, there are total 8 persons. We have to select 5 among them.
Total number of ways =8C5
Statements:
1) All grasses are trees.
2) No tree is shrub.
Conclusions:
1) No grasses are shrubs.
2) Some shrubs are grasses.
G ⇒ Grasses
T⇒Trees
S ⇒Shrubs
Clearly only statement 1 is true.
To chatter is to talk rapidly, and to flutter is to flap rapidly.
Flower is a subset of bouquet
Page is a subset of book....
But Gallon doesn't belong to quintal.
Hence, option A is the correct answer.
How many words can be formed with the letters of the word ′OMEGA′ such that O and A occupy end places
O_ _ _ _ _A
The three letters can be arranged in 3!=6 while o and a can exchange their places.
Number of ways =3!×2!=12
Laugh indicates joy similarly weep indicates grief
Four numbers are given below out of which three are alike in some manner and fourth is different. Choose the different number :
All are perfect squares except 168
Hence, option B is the odd one out.
The reciprocal ratio of a:b is b:a
∴ reciprocal ratio of 21:31 is 31:21
The new matrix obtained after adding 2nd row to 3 times 3rd row is
Pointing towards a man in the photograph. Archana said 'He is the son of the only son of my grandmother'. How is man related to Archana?
The given statement says, 'He is the son of the only son of my grandmother'.
Only son of Archana's grandfather means Archana's father
His son is Archana's brother.
Tiya has Rs.59. She buys a comic book for Rs.32Rs.32. How much money is left with her?
⇒ Tiya has Rs.59.
⇒ Money spend on comic book =Rs.32.
∴ Money left with Tiya =Rs.59−Rs.32=Rs.27.
∴ Money left with Tiya is Rs.27
If Set P= Set M, this means they wll have the same elements.
So, the number of elements in the sets will also be the same.
Hence, n(P)=n(M)
If R is relation from a finite set A having m elements to a finite set B having n elements, then the number of relations from A to B is
A×B will have mn ordered pairs. Each subset of
A×B will be relation. The number of subsets of a
set consisting of mn elements will be 2mn.
Note : If m=n,then corresponding number will be 2n2.
Pttern is 3,3×3,9×3,27×3......
∴ Misssing number = 81×3=243
In a certain code language, '324' means 'Light is bright', '629' means 'Girl is beautiful' and '4758' means 'I prefer bright clothes'. Which digit means 'Light' in that language?
In the first and second statement, we find that '2' means 'is'. In the first and third statement, we find that '4' means 'bright'. Thus in the first statement, '3' means 'light'.
Hence, option (A) is the correct answer.
Who amongst P, Q, R, S T and U is the tallest?
I. P is taller than R and T, but not as tall as U, who is taller than Q and S.
II. R is the third in the height in the ascending order and not as tall as U, P and Q, Q being taller than P but not the tallest.
Clearly,
Everyone is shorter than U from statement I. Thus, U is tallest.
Given, g(x)=x2
We have to calculate g(−2)
Putting −2 in place of x, we get
g(−2)=(−2)2=4
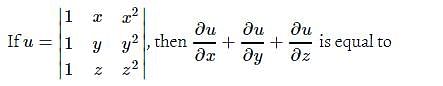
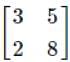Choose the correct option about conclusion drawn from the statements given below.
Statements:
Some actors are singers.
All the singers are dancers.
Conclusions:
1. Some actors are dancers.
2. No singer is actor.
Understanding the code, PITCH = SLWFK, find the correct code language for the word 'BLASTER', from the given alternatives.
In the following question, there are four options. Three numbers, in these options, are alike in certain manner. Only one number does not fit in. Find the one which doesn't fit.
In all other group of letters except D, third and second letters are consecutive whereas first letter is 3 steps ahead from the second in alphabetic series.
But in D, 3rd and 2nd letters are consecutive whereas 1st and 2nd letters differ by +4.
Hence, the group of letters in D is different from others.
In exponent form
(x+5)=101
∴x=10−5=5
If A = 
then which of the following is not an element of A?
0 is not present in given matrix.
Option A is correct.
f is a function from set A to set B, Then A is called .........
f:A→B
A is called the domain of the function f:A→B.
B is the range of function.
All others are underground vegetables.
If air is called water, water is called green, green is called dust, dust is called yellow and yellow is called cloud, which of the following does fish live in ?
We know that fish lives in water, but it is given that water is called green.
Therefore, fish lives in green.
Hence, option C is the correct answer.
log18
=log6×3
=log6+log3
Hence, A is the correct option.
Write the following set in the set builder form.
F={I,N,D,A}
Clearly these are letters of the word INDIA.
∴F={x|x is letter of the word INDIA.}
A graph may be defined as a set of points connected by lines called edges. Every edge connects a pair of points. Thus, a triangle is a graph with 3 edges and 3 points. The degree of a point is the number of edges connected to it. For example, a triangle is agraph with three points of degree 2 each. Consider a graph with 12 points. It is possible to reach any point from any other point through a sequence of edges. The number of edges "e" in the graph must satisfy the condition
Statements:
1. All pens are pencils.
2. No pencil is a monkey.
Conclusions:
I. No pen is a monkey.
II. some pens are monkeys.
III. All monkeys are pens.
From the statements
1. All pens are pencils.
2. No pencil is a monkey.
And From Conclusions
Conclusions:
I. No pen is a monkey.
II. some pens are monkeys.
III. All monkeys are pens.
It is clear that No pen is monkey because from statement it is clear that all pens are pencils
And from Statement two it is clear that no pencil are monkey
Since all pens are pencil's it apply that no pens are monkey
The mean of 13 observations is 14. If the mean of the first 7 observations is 12 and that of the last 7 observations is 16, then the 7th observation is ___________.
Sum of all observations =13×14=182
Sum of the first 7 observations =7×12=84
Sum of the last 7 observations=7×16=112
Sum of the first 7 observations + Sum of the last 7 observations = sum of total terms + 7th term$$
⇒84+112=182+7th term
Therefore, 7th term =196−182=14
Mean deviation, standard deviation as well as quartile deviation is the measure of dispersion.
Hence, all of these are measure of dispersion.
(It is well known fact)
The histogram, given alongside, shows the heights of students (in centimetre) and their numbers.
Use the given histogram to answer the following :
Q. How many students have their height less than 140 cm ?
Number of students in (125 cm −130 cm)=6
Number of students in (130 cm −135 cm)=8
Number of students in (135 cm −140 cm) =20
So, total number of students less than 140 cm. =20+6+8=34
If the sum of the mode and mean of the certain frequency distribution in 129 and the median of the observations is 63, mode and mean are respectively
Given, Mode+ Mean = 129 .....(1)
and Median =63,
Also we know, Mode = 3. Median − 2. Mean
⇒ Mode=3×63−2. Mean =129−2.Mean ..(2)
Solving (1) and (2) we get, Mean=60 and Mode =69.
_______ are also used in marketing, monitoring, policy development, bench marking, for lobbying, for the planning of services and for internal research purposes.
Statistics are also used in marketing, monitoring, policy development, bench marking, for lobbying, for the planning of services and for internal research purposes.
Example: Refer diagram
The median of a given frequency distribution is found graphically with the help of
The median of a given frequency distribution is found graphically with the help of ogive.
This can be done in two ways:
(i) Presenting the data graphically in the form of 'less than' ogive or 'more than' ogive .
(ii) Presenting the data graphically and simultaneously in the form of 'less than' and 'more than' ogives. in this graph two ogives are drawn together.
Hence, option D is correct.
If the median of 
is 8 then the value of x would be
Tally marks are used for counting. They represent frequrncy
The A.M. of a set of 50 numbers is 38. If two numbers of the set, namely 55 and 45 are discarded, the A.M. of the remaining set of numbers is :
Which frequency curve is correct for the following histogram?
In histogram, the height of rectangle shows _____
A histogram is a display of statistical information that uses rectangles to show the frequency of data items in successive numerical intervals of equal size.
Hence, height of the rectangle represents the frequency of the class.
If the coefficient of variation and standard deviation of a distribution are 50% and 20 respectively, the its mean is
A student got marks in 5 subjects in a monthly test is given below: 2,3,4,5,6.In these obtained marks, 4 is the
Given that bar with lines in the people reading newspaper and the empty bar is the people watching TV.
From the given graph, for the city Chennai, we can observe that the height of the empty bar is 40.
Therefore, Chennai has 40 people who watch TV.
integers from −4 to +5 are =−4,−3,−2,−1,0,1,2,3,4,5
sum of all these integers =5
total elements =10
so mean =5/10=0.5
If the average marks of three batches of 55, 60 and 45 students respectively is 50, 55, 60, then the average marks of all the students is:
The sum of the squares deviations for 10 observations taken from their mean 50 is 250. The coefficient of variation is
The given bar graph shows the marks obtained by a student in different subjects. The maximum marks of each subject is 100.
Q. In which subject did the student score highest marks?
Given graph shows the marks obtained in different subjects.
From the graph, the highest marks are 90 which is obtained in Mathematics
For a certain frequency distribution, the value of Mean is 101 and Median is 100. Find the value of Mode.
We have
Mean =101
Median =100
We know that,
Mean − Mode = 3(Mean − Median)
101− Mode =3(101−100)
100− Mode =3
101−3= Mode
Mode =98
The sale of salesman in a week are given below in the pie diagram. Study the diagram and answer the following questions, if the total sale due to salesman A is Rs. 18,000.
Q. The salesman with the highest sale is:
In a given pie chart, Salesman B has the greatest angle i.e. 120° when compared to other salesmen.
Also, we know that in a circle, greater the angle of an arc, greater the area.
∴ Salesman B has the highest sale.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
The sum of the squares of deviations of 10 items about mean 50 is 250 .The coefficient of variation is
The histogram shows the number of music directors and the number of songs they complete in a year.
Q. Find the number of songs made during the interval 5−6.
The height of the bar represents the number of songs.
So, total of 20 songs made during the interval 5−6.
The mean square deviation of set of n observations x1, x2,........ xn. about a point c is defined as
The mean square deviation about —2 and 2 are 18 and 10 respectively, then standard deviation of this set of observations is
If the difference of Mode and Median of a data is 24, then the difference of Median and Mean is
We have,
Mode=3Median−2Mean
⇒Mode−Median=2(Median−Mean)
⇒24=2(Median−Mean)⇒Median−Mode=12
A survey was carried out for the purpose of determining the number of children in each family. The results are shown in the table below. Calculate the percentage of families which have more than 2 children.
On 13 consecutive days the number of person booked for violating speed limit of 40 km/hr. were as follows
59,52,58,61,68,57,62,50,55,62,53,54,51.
Q. The median number of speed violations per day is
⇒ In the above given data 62 is repeated twice,
⇒ Now we write the data in ascending order.
⇒ 50,51,52,53,54,55,57,58,59,61,62,62,68
⇒ Thus, the measure of (13+1)/2 = 7th number is median value.
∴ The median number of speed violation per day is 57.
What are the objectives of measure of dispersion?
Objectives of measure of dispersion:
(i)Reliability of measure of central tendency
(ii)Control of variability
(iii)Helpful in use of further statistical analysis as in regression, correlation etc
What is the arithmetic mean of first 16 natural numbers with weights being the number itself?
Class 0−10 has lowest frequency i.e. 1.
There are 30 students in a class. The average age of the first 10 students is 12.5 years. The average age of the remaining 20 students is 13.1 years. What is the average age (in years) of the students of the whole class?
Read the above graph and answer the question given below
At what subject is the student sharp
Mathematics as its has highest peak
If M and Mg represents the mean of the raw and grouped data respectively then
We know that mode=3median−2mean
Given that mean=10 and mode=10
Therefore, 10=3median−2(10)
⟹3median=10+20
⟹median=30/3=10
Here, the highest frequency of receiving letters is 80.
So, the mode is 480.
If mean deviation about Mean of a particular data consisting 10 observations is7, then what will be value of mean deviation when each is multiplied by 5?
Suppose original numbers were : x1 , x2, x3, ……, xn
Thus, (x1+x2+x3+…….+xn)/n=10 (by the very definition of mean
After adding 1 to each number, the sum would be : 5× (x1+x2+x3+…….+xn)+n
Thus new mean would be: (5×(x1+x2+x3+…….+xn)+n)/n=5×10+1=51
Read the shown graph and answer the questions. Highest marks are scored in the subject
Answer:-- Converting the graph into frequency distribution table
Subject Marks
English 15
Hindi 10
Math 25
The maximum frequency is of maths. i.e. 25.
Find the mean of the data x,x+a,x+2a,x+3a,...
[(2n+1)terms]
Assertion
If mean & median of an asymmetrical distribution are 58 & 61respectively, then Mode =67.
Reason
For an asymmetrical distribution Mode = 3 Median -2 Mean .
∵ Mode =3 Median −2 Mean
given, Mean=58 Median=61
Thus Mode=3×61−2×58=67
Hence Assertion & Reason bth are correct and Reason is correct explanation of Assertion.
|
83 docs|19 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
83 docs|19 tests
|
Download free EduRev App
Related content with Business Mathematics Mock Test - 2
|
|
Related tests with Business Mathematics Mock Test - 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
