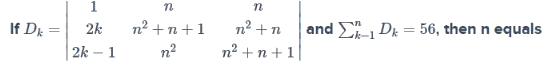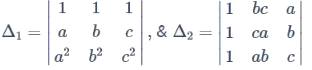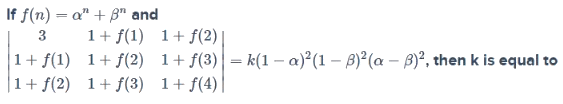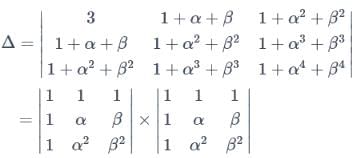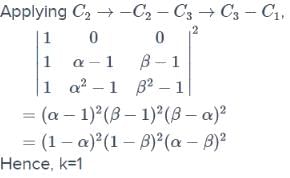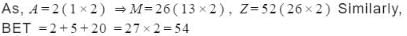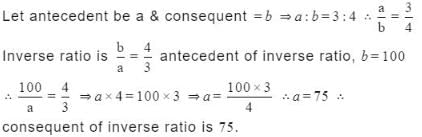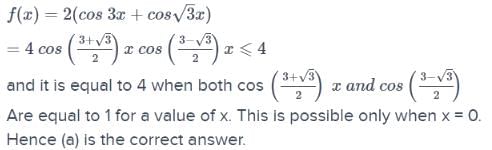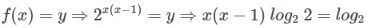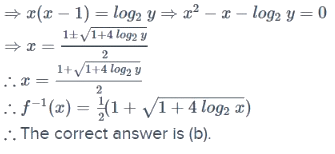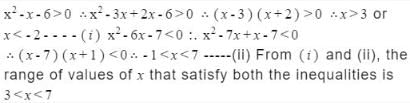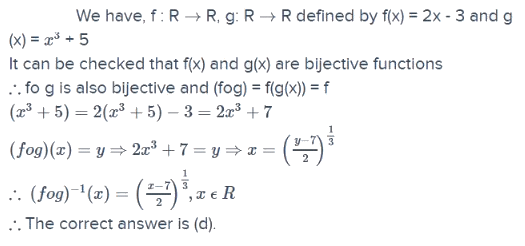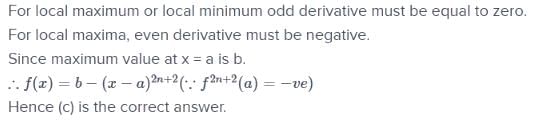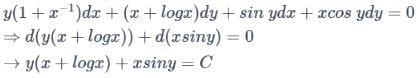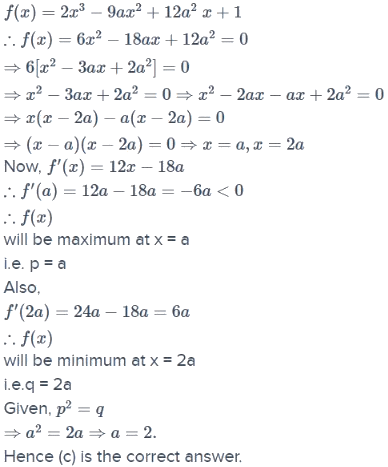Quantitative Aptitude Mock Test - 3 - CA Foundation MCQ
30 Questions MCQ Test Mock Tests & Past Year Papers for CA Foundation - Quantitative Aptitude Mock Test - 3
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If sin y = x sin (a + y) and 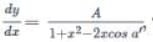 then the value of A is
then the value of A is
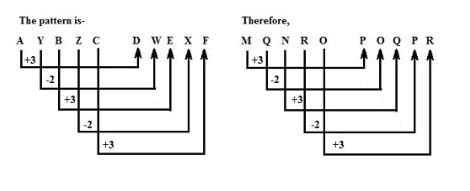
Complete the given series.
AYBZC, DWEXF, GUHVI, JSKTL, (?), POQPR
If x and y are two unequal positive numbers, then which of the following is definitely true?
If A = 2, M = 26, Z = 52, then BET will be equal to
The ratio of two quantities is 3:4. if the antecedent of its inverse ratio is 100, then its consequent is
The annual gathering of a college was organised on a day. Six different programmes - drama , singing , mimicry ,speech , story -telling and dance are to be performed by six student A , B , C , D , E , and F , not necessarily in the same order. the programme begins with a song not sung by B and ends with a dance. C performs mimicry immediately after the speech. E performs drama just before the dance. D or F are not available for the last performance. The speech is not given by A. An interval of 30 minutes is given immediately after mimicry with three more items remaining to be performed . D performs immediately after the interval .
Q. Which items is performed by F ?
If the angles of a triangle are in the ratio 2 : 7 : 11, then their respective degree measures are
The number of values of x where the function f(x) = 2 (cos 3x + cos √3x attains itsmaximum, is
If the function f : [1,∞) → [1,∞) is defined by f (x) = 2x(x-1), then f-1(x) is
A function y =f(x) has a second order derivative f"=6(x-1). If its graph passes through the point(2,1) and at that point the tangent to the graph is y =3x -5, then the function is
Find the range of values of x that satisfy the inequalities x2-x-6>0 and x2-6x-7<0
Let f: R → R, g: R → R, be two functions, such that f(x) = 2x - 3, g (x) = x3 + 5 the function (fog)-1 (x) is equal to
A function f such that f (a) = f"(a) = ........... f2n (a) = 0 and f has a local maximum value b at x = a, if f(x) is
The solution of (y(1 + x-1) + siny) dx + (x + logx + x cosy) dy = 0 is
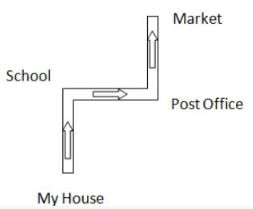
The post office is to the east of the school while my house is to the south of the school. The market is to the north of the post office. If the distance of the market from the post office is equal to the distance of my house from the school, then in which direction is the market with respect to my school?
Directions: Read the given information carefully and answer the question given beside:
Eight people Aarush, Bindu, Chunnu, Divya, Etti, Prithvi, Gopal and Harish live in an eight storey building, but not necessarily in the same order. The lowermost floor is numbered 1 and the topmost floor is numbered 8.
Aarush lives on an even-numbered floor but not on the floor numbered second or fourth. Only three floors are there between Aarush and Bindu. Only two people live between Chunnu and Etti. Prithvi lives on a floor above Divya. There are equal numbers of floors between the floors on which Etti and Bindu live and between the floors on which Aarush and Etti live. Harish lives immediately below Divya’s floor. Gopal lives immediately below Aarush’s floor.
Q. Prithvi lives on which of the following floors?
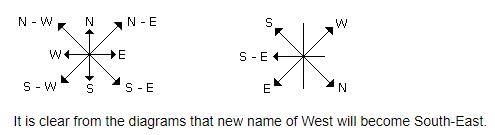
If South-East becomes North, North-East becomes West and so on. What will West become?
If the function f(x) = 2x3 - 9ax2 + 12a2 x + 1, where a> 0, attains its maximum and minimum at p and q respectively such that p2 = q, then a equals
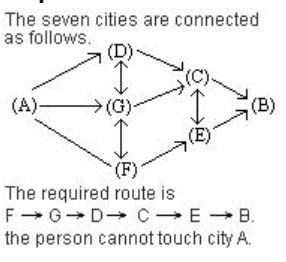
Seven cities - A, B, C, D, E, F and G are connected as follows. The cities which are connected by one way route are as follows. A to D, C to B, G to C, F to E, E to B, A to F , D to C and A to G. The cities which are connected by two way routes are as follows. C and E; G and F; D and G.
If a person, who has to reach city B, stared his Journey from city F touching the maximum possible number of cities exactly once, then which city he cannot touch?
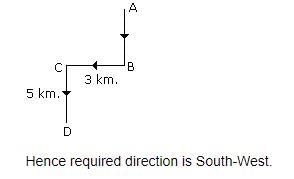
A man walks 5 km toward south and then turns to the right. After walking 3 km he turns to the left and walks 5 km. Now in which direction is he from the starting place?
|
127 docs|19 tests
|
|
127 docs|19 tests
|


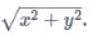 Then, f is
Then, f is