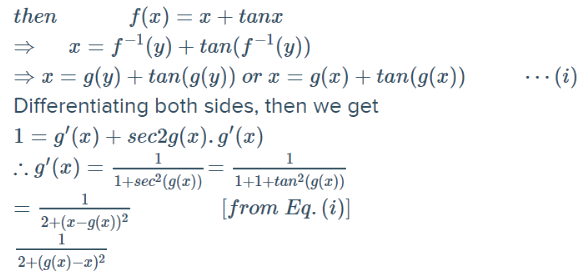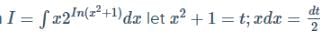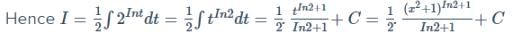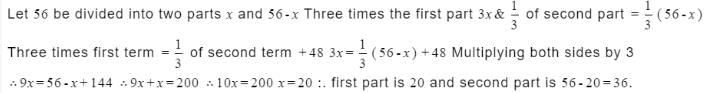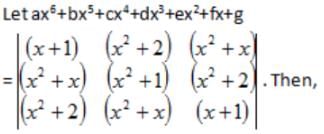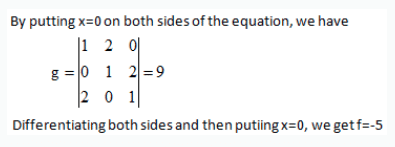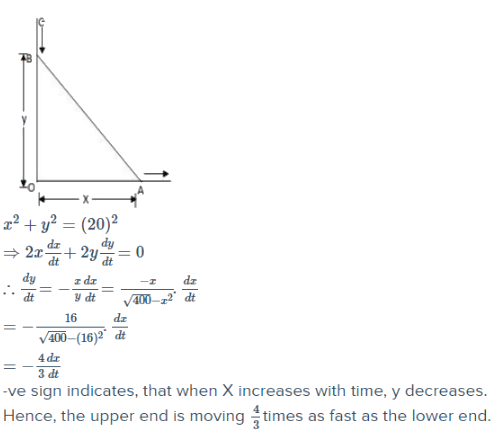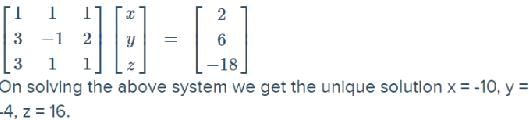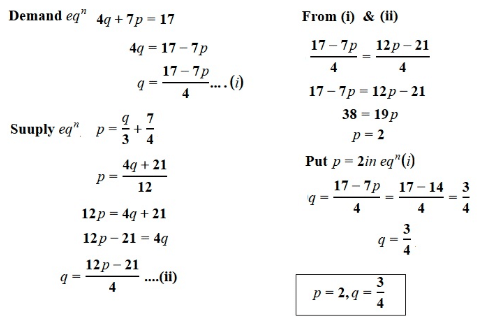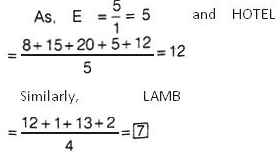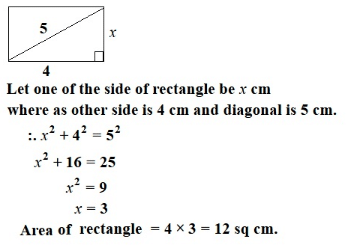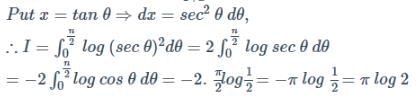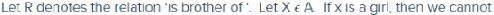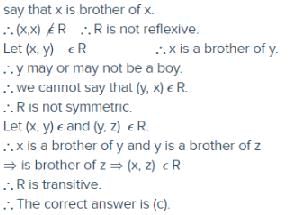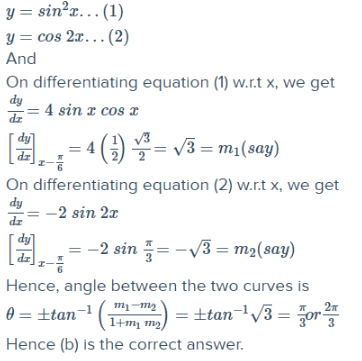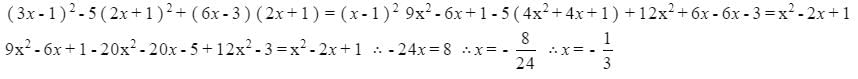Quantitative Aptitude Mock Test - 7 - CA Foundation MCQ
30 Questions MCQ Test - Quantitative Aptitude Mock Test - 7
If the system of linear equation x+2ay+az = 0, x+3by+bz = 0, x+4cy+cz = 0 has a non zero solution, then a, b,c
If f(x) = x + tan x and f is inverse of g, then g’(x) is equal to
Primitive of f(x) = x.2 In (x2 + 1) with respect to x is
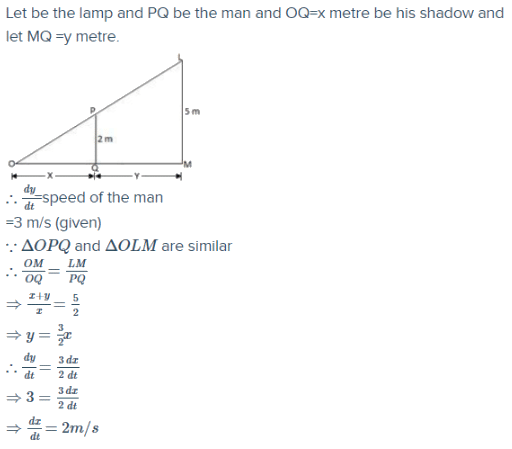
A man of height 2m walks directly away from a lamp of height 5m, on a level road at 3 m/s. The rate at which the length of his shadow is increasing is
Divide 56 into two parts such that three times the first part exceeds one-third of the second by 48. Then the two parts are
A ladder20 ft long has one end on the ground and the other end in contact with a vertical wall. The lower end slips along the ground. If the lower end of the ladder is 16 ft away from the wall, upper end is moving λ times as fast as the lower end, then λ is
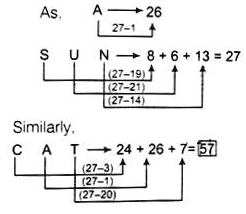
If A = 26, SUN = 27, then CAT will be equal to
If 'green' is called 'white', 'white' is called 'yellow', 'yellow' is called 'red', 'red' is called 'orange', then which of the following represents the colour of sunflower?
Let X be a family of sets and R be a relation on X defined by 'A is disjoint from B'. Then R is
The system of equations x + y + z =2, 3x − y + 2z =6 and 3x + y + z =−18 has
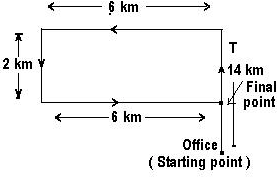
Ranjeev started from his office on duty. After traveling straight for a distance of 14 Km, he turned left for the market and traveled straight for 6 Km. He now turned left again and traveled another 2 Km, and then again left and traveled straight for 6 Km. How far is Ranjeev from office?
The demand and supply equations of a certain commodity are 4q+7p=17 and p= q/3+7/4 respectively, where p is the market price and q is the quantity. Then the equilibrium price and quantity are respectively
If E = 5 and HOTEL = 12, how will you code LAMB?
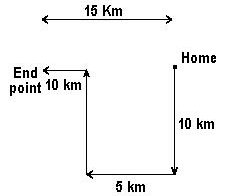
One day Anuneet left home and cycled 10 Km southwards, turned right and cycled 5 Km and turned right and cycled 10 Km and left and cycled 10 Km. How many Kms will he have to cycle to reach his home straight?
If the diagonal of a rectangle is 5 cm and one of its sides is 4 cm, then its area is
Let A be the non – empty set of children in a family. The relation ‘x is a brother of y’ in A is
The slope of the tangent to the curve x=t2+3t−8, y=2t2−2t−5 at the point t = 2 is
A boy starts walking straight towards the north and walks 10 feet, then he turns to his left and walks 5 feet, then he turns to his left and walks another 5 feet, then again he turns to his left and walks 10 feet and then turns to his right and walks 2 feet. How far is he now from his starting point?
Who is between the Lawyer and the Business Analyst?
The angle of intersection of the curves y=2sin2 x and y= cos 2x at x =π/6 is
Six persons Amit, Amitabh, Arnold, Aakash, Abhinav and Atul, each of a different profession, among Docot, Lawyer, Teacher, Manager, Business Analyst and Accountant, are seated around a table in six equi-spaced chairs. Atul is opposite to the Lawyer. Arnold is to the right of the Doctor and is opposite the person who is the Business Analyst. Aakash is opposite the Accountant. Abhinav is between the Manager and the Accountant and is not the Business Analyst. Amitabh is opposite the Manager, who is the left of Aakash.
Q. If Amitabh is the Business Analyst, then who is opposite Amitabh?
Six persons Amit, Amitabh, Arnold, Aakash, Abhinav and Atul, each of a different profession, among Docot, Lawyer, Teacher, Manager, Business Analyst and Accountant, are seated around a table in six equi-spaced chairs. Atul is opposite to the Lawyer. Arnold is to the right of the Doctor and is opposite the person who is the Business Analyst. Aakash is opposite the Accountant. Abhinav is between the Manager and the Accountant and is not the Business Analyst. Amitabh is opposite the Manager, who is the left of Aakash.
Q. Which of the following statements is false?
The value of x which satisfies the equation (3x-1)2-5(2x+1)2+(6x-3)(2x+1)=(x-1)2 is