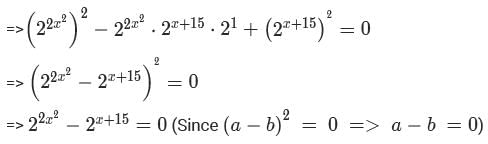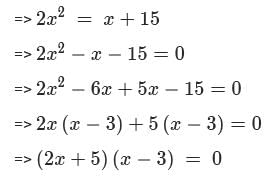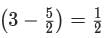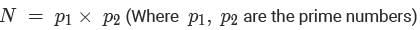CAT 2023 Slot 2 Question Paper (July 30) - CAT MCQ
15 Questions MCQ Test Daily Test for CAT Preparation - CAT 2023 Slot 2 Question Paper (July 30)
All of the following, if true, can weaken the passage’s claim that facts do not speak for themselves, EXCEPT:
According to this passage, which one of the following statements best describes the significance of archaeology for historians?
If the author of the passage were to write a book on the Battle of Hastings along the lines of his/her own reasoning, the focus of the historical account would be on:
Based on information provided in the passage, all of the following are true, EXCEPT:
The author sees the rise of Netflix in Europe as:
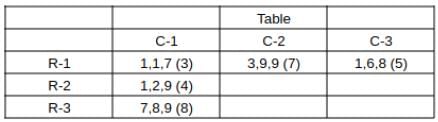
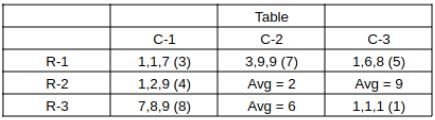
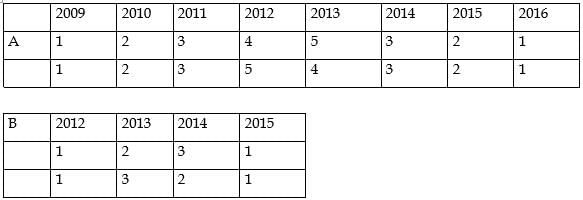
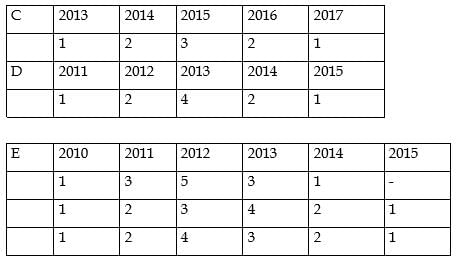
What is the total number of coins in all the boxes in the 3rd row?
How many boxes have at least one sack containing 9 coins?
For how many boxes are the average and median of the numbers of coins contained in the three sacks in that box the same?
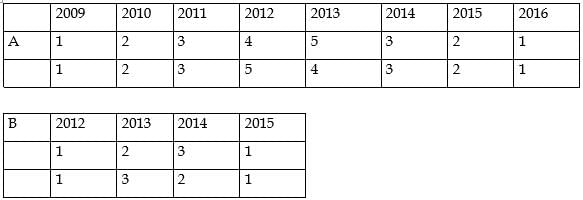
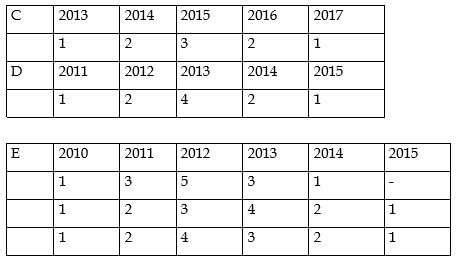
For which firm(s) can the amounts raised by them be concluded with certainty in each year?
What best can be concluded about the total amount of money raised in 2015?
Let a, b, m and n be natural numbers such that a> 1 and . If ambn = 144145, then the largest possible value of n-m is
Any non-zero real numbers x,y such that y ≠ 3 and 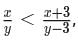 Will satisfy the condition.
Will satisfy the condition.
For any natural numbers m, n, and k, such that k divides both m+2n and 3m + 4n, k must be a common divisor of
The sum of all possible values of x satisfying the equation 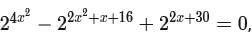 is
is
The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is
|
152 docs|327 tests
|




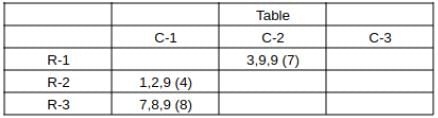
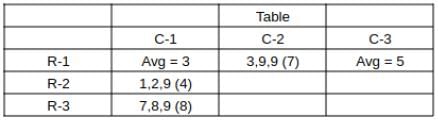












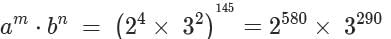


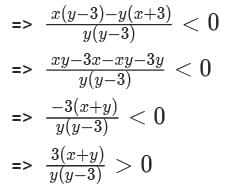
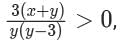
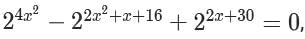 which can be written as:
which can be written as: