CAT Mock Test- 10 (November 12) - CAT MCQ
30 Questions MCQ Test Daily Test for CAT Preparation - CAT Mock Test- 10 (November 12)
Read the passage and answer the following questions:
To better understand how the brain underlies selfhood, we need to understand its complex form; its intricate structure at the level of connections between neurons. After all, understanding biological structure has revealed the nature of many diverse life forms. Plants thrive because their typically broad leaves are perfect for transducing light energy into vital chemical energy. Similarly, eyes, whether human or insect, enable the transduction of light from one’s surroundings into electrical signals within the nervous system. These impulses carry information that represents features of the surrounding environment. But when it comes to the relationship between structure and function, brains have remained an enigma. There’s a lot more to them than to other organs that have specific functions, such as eyes, hearts or even hands. These organs can now be surgically replaced. Yet, even if a brain transplant were possible, you couldn’t just switch your brain with another person’s and maintain the same mind. Upon birth, a person’s brain structure is largely prescribed by experience in the womb and their unique genetic code. As we age, experience continues to imprint unique changes on the brain’s neural connectivity, increasing connections in some areas while decreasing them in others, accumulating reroutes upon reroutes as a person ages and learns, gaining knowledge and experience. Additionally, there are alterations in the strength of existing connections. These processes are especially evident in twins, whose brains are strikingly similar when born. However, as they grow, learn and experience the world, their brains diverge, and their essential selves become increasingly unique.
Although there are indeed anatomical regions that appear to serve relatively specific functions, one’s memory is not formed, stored or recalled within the activity of any single brain region. Certain structures, such as the amygdala and the hippocampus, play key roles but trying to find memory in one specific area is simply impossible. It would be like trying to listen to Beethoven’s Fifth but hearing only the strings. Instead, memory, in its broadest sense, lies in the uniqueness of a brain’s entire connective structure, known as the connectome. The connectome consists of its complete network of neurons and all the connections between them, called synapses. It is argued that, fundamentally, ‘you are your connectome’.
Mapping a connectome at the level of single neurons, however, is currently impossible in a living animal. Instead, animal brains must be extracted, perfused with a fixative such as formaldehyde and sliced up as many times as possible before being analysed structurally in order to painstakingly find individual neurons and trace their paths. To achieve this, the properties of each new slice are recorded using various microscopy techniques. Once that’s been done, patterns of electrical flow can be estimated from different neuron types and from connections that excite or inhibit other neurons. What’s crucial is that the extracted brain is preserved accurately enough to maintain its intricate, complex connectome before it’s sliced up.
Currently, it’s unlikely that any human brain has been preserved with its entire connectome perfectly intact as our brains degrade too quickly after death.
The author mentions the example of plants and eyes at the beginning to...
To better understand how the brain underlies selfhood, we need to understand its complex form; its intricate structure at the level of connections between neurons. After all, understanding biological structure has revealed the nature of many diverse life forms. Plants thrive because their typically broad leaves are perfect for transducing light energy into vital chemical energy. Similarly, eyes, whether human or insect, enable the transduction of light from one’s surroundings into electrical signals within the nervous system. These impulses carry information that represents features of the surrounding environment. But when it comes to the relationship between structure and function, brains have remained an enigma. There’s a lot more to them than to other organs that have specific functions, such as eyes, hearts or even hands. These organs can now be surgically replaced. Yet, even if a brain transplant were possible, you couldn’t just switch your brain with another person’s and maintain the same mind. Upon birth, a person’s brain structure is largely prescribed by experience in the womb and their unique genetic code. As we age, experience continues to imprint unique changes on the brain’s neural connectivity, increasing connections in some areas while decreasing them in others, accumulating reroutes upon reroutes as a person ages and learns, gaining knowledge and experience. Additionally, there are alterations in the strength of existing connections. These processes are especially evident in twins, whose brains are strikingly similar when born. However, as they grow, learn and experience the world, their brains diverge, and their essential selves become increasingly unique.
Although there are indeed anatomical regions that appear to serve relatively specific functions, one’s memory is not formed, stored or recalled within the activity of any single brain region. Certain structures, such as the amygdala and the hippocampus, play key roles but trying to find memory in one specific area is simply impossible. It would be like trying to listen to Beethoven’s Fifth but hearing only the strings. Instead, memory, in its broadest sense, lies in the uniqueness of a brain’s entire connective structure, known as the connectome. The connectome consists of its complete network of neurons and all the connections between them, called synapses. It is argued that, fundamentally, ‘you are your connectome’.
Mapping a connectome at the level of single neurons, however, is currently impossible in a living animal. Instead, animal brains must be extracted, perfused with a fixative such as formaldehyde and sliced up as many times as possible before being analysed structurally in order to painstakingly find individual neurons and trace their paths. To achieve this, the properties of each new slice are recorded using various microscopy techniques. Once that’s been done, patterns of electrical flow can be estimated from different neuron types and from connections that excite or inhibit other neurons. What’s crucial is that the extracted brain is preserved accurately enough to maintain its intricate, complex connectome before it’s sliced up.
Currently, it’s unlikely that any human brain has been preserved with its entire connectome perfectly intact as our brains degrade too quickly after death.
Read the passage and answer the following questions:
To better understand how the brain underlies selfhood, we need to understand its complex form; its intricate structure at the level of connections between neurons. After all, understanding biological structure has revealed the nature of many diverse life forms. Plants thrive because their typically broad leaves are perfect for transducing light energy into vital chemical energy. Similarly, eyes, whether human or insect, enable the transduction of light from one’s surroundings into electrical signals within the nervous system. These impulses carry information that represents features of the surrounding environment. But when it comes to the relationship between structure and function, brains have remained an enigma. There’s a lot more to them than to other organs that have specific functions, such as eyes, hearts or even hands. These organs can now be surgically replaced. Yet, even if a brain transplant were possible, you couldn’t just switch your brain with another person’s and maintain the same mind. Upon birth, a person’s brain structure is largely prescribed by experience in the womb and their unique genetic code. As we age, experience continues to imprint unique changes on the brain’s neural connectivity, increasing connections in some areas while decreasing them in others, accumulating reroutes upon reroutes as a person ages and learns, gaining knowledge and experience. Additionally, there are alterations in the strength of existing connections. These processes are especially evident in twins, whose brains are strikingly similar when born. However, as they grow, learn and experience the world, their brains diverge, and their essential selves become increasingly unique.
Although there are indeed anatomical regions that appear to serve relatively specific functions, one’s memory is not formed, stored or recalled within the activity of any single brain region. Certain structures, such as the amygdala and the hippocampus, play key roles but trying to find memory in one specific area is simply impossible. It would be like trying to listen to Beethoven’s Fifth but hearing only the strings. Instead, memory, in its broadest sense, lies in the uniqueness of a brain’s entire connective structure, known as the connectome. The connectome consists of its complete network of neurons and all the connections between them, called synapses. It is argued that, fundamentally, ‘you are your connectome’.
Mapping a connectome at the level of single neurons, however, is currently impossible in a living animal. Instead, animal brains must be extracted, perfused with a fixative such as formaldehyde and sliced up as many times as possible before being analysed structurally in order to painstakingly find individual neurons and trace their paths. To achieve this, the properties of each new slice are recorded using various microscopy techniques. Once that’s been done, patterns of electrical flow can be estimated from different neuron types and from connections that excite or inhibit other neurons. What’s crucial is that the extracted brain is preserved accurately enough to maintain its intricate, complex connectome before it’s sliced up.
Currently, it’s unlikely that any human brain has been preserved with its entire connectome perfectly intact as our brains degrade too quickly after death.
Which of the following sentences is/are true as per the passage?
To better understand how the brain underlies selfhood, we need to understand its complex form; its intricate structure at the level of connections between neurons. After all, understanding biological structure has revealed the nature of many diverse life forms. Plants thrive because their typically broad leaves are perfect for transducing light energy into vital chemical energy. Similarly, eyes, whether human or insect, enable the transduction of light from one’s surroundings into electrical signals within the nervous system. These impulses carry information that represents features of the surrounding environment. But when it comes to the relationship between structure and function, brains have remained an enigma. There’s a lot more to them than to other organs that have specific functions, such as eyes, hearts or even hands. These organs can now be surgically replaced. Yet, even if a brain transplant were possible, you couldn’t just switch your brain with another person’s and maintain the same mind. Upon birth, a person’s brain structure is largely prescribed by experience in the womb and their unique genetic code. As we age, experience continues to imprint unique changes on the brain’s neural connectivity, increasing connections in some areas while decreasing them in others, accumulating reroutes upon reroutes as a person ages and learns, gaining knowledge and experience. Additionally, there are alterations in the strength of existing connections. These processes are especially evident in twins, whose brains are strikingly similar when born. However, as they grow, learn and experience the world, their brains diverge, and their essential selves become increasingly unique.
Although there are indeed anatomical regions that appear to serve relatively specific functions, one’s memory is not formed, stored or recalled within the activity of any single brain region. Certain structures, such as the amygdala and the hippocampus, play key roles but trying to find memory in one specific area is simply impossible. It would be like trying to listen to Beethoven’s Fifth but hearing only the strings. Instead, memory, in its broadest sense, lies in the uniqueness of a brain’s entire connective structure, known as the connectome. The connectome consists of its complete network of neurons and all the connections between them, called synapses. It is argued that, fundamentally, ‘you are your connectome’.
Mapping a connectome at the level of single neurons, however, is currently impossible in a living animal. Instead, animal brains must be extracted, perfused with a fixative such as formaldehyde and sliced up as many times as possible before being analysed structurally in order to painstakingly find individual neurons and trace their paths. To achieve this, the properties of each new slice are recorded using various microscopy techniques. Once that’s been done, patterns of electrical flow can be estimated from different neuron types and from connections that excite or inhibit other neurons. What’s crucial is that the extracted brain is preserved accurately enough to maintain its intricate, complex connectome before it’s sliced up.
Currently, it’s unlikely that any human brain has been preserved with its entire connectome perfectly intact as our brains degrade too quickly after death.
Read the passage carefully and answer the following questions:
We must dispense with the idea that democracy is like a torch that gets passed from one leading society to another. The core feature of democracy - that those who rule can do so only with the consent of the people - wasn’t invented in one place at one time: it evolved independently in a great many human societies. Over several millennia and across multiple continents, early democracy was an institution in which rulers governed jointly with councils and assemblies of the people. Classical Greece provided particularly important instances of this democratic practice, and it’s true that the Greeks gave us a language for thinking about democracy, including the word demokratia itself. But they didn’t invent the practice. The core feature of early democracy was that the people had power, even if multiparty elections didn’t happen. The people, or at least some significant fraction of them, exercised this power in many different ways. In some cases, a ruler was chosen by a council or assembly, and was limited to being first among equals. In other instances, a ruler inherited their position, but faced constraints to seek consent from the people before taking actions both large and small.
The first difference between early democracy and our democracies today is that this earlier form of rule was a small-scale phenomenon. In Classical Athens those who had the right to participate in politics tended to do so in a very direct and intensive way, particularly in local assemblies. In modern democracy, participation is very broad, but it’s also not deep; for most of us, it’s limited to voting in elections every few years, and in between these moments others make the decisions. The potential risk of this arrangement, as has been noted by astute observers since the birth of modern republics, is that citizens might grow distrustful of the people who are actually running government on a daily basis and of the special influences to which they might be subject. One way to address the problem of scale is to delegate much more power to states, provinces and localities. But on crucial issues of foreign trade, diplomacy or pressing constitutional questions, it’s impractical for individual states, regions or provinces to set their own policy. If large scale has the potential to lead to distrust and disengagement in a democracy, then a closely related problem is that of polarisation, which can take many forms, such as that involving tensions between different classes of people in the same location, or a difference of opinions between people living in different locations.
The absence of a state bureaucracy was a chief reason why early democracy proved to be such a stable form of rule for so many societies. With little autonomous power - apart from the ability to persuade - those who would have liked to rule as autocrats found themselves without the means to do so. The flipside of this was that, in many early democracies, those who were unhappy with a central decision could simply refuse to participate or even decamp to a new locality. Modern democracy lacks the same protections from central power that early democracies enjoyed. At the same time, having a powerful central state can allow a society to achieve goals such as universal education and prosperity, to name but a few. The question then is how to live with a state while preserving democracy.
Which of the following is the author of the passage most likely to agree with?
We must dispense with the idea that democracy is like a torch that gets passed from one leading society to another. The core feature of democracy - that those who rule can do so only with the consent of the people - wasn’t invented in one place at one time: it evolved independently in a great many human societies. Over several millennia and across multiple continents, early democracy was an institution in which rulers governed jointly with councils and assemblies of the people. Classical Greece provided particularly important instances of this democratic practice, and it’s true that the Greeks gave us a language for thinking about democracy, including the word demokratia itself. But they didn’t invent the practice. The core feature of early democracy was that the people had power, even if multiparty elections didn’t happen. The people, or at least some significant fraction of them, exercised this power in many different ways. In some cases, a ruler was chosen by a council or assembly, and was limited to being first among equals. In other instances, a ruler inherited their position, but faced constraints to seek consent from the people before taking actions both large and small.
The first difference between early democracy and our democracies today is that this earlier form of rule was a small-scale phenomenon. In Classical Athens those who had the right to participate in politics tended to do so in a very direct and intensive way, particularly in local assemblies. In modern democracy, participation is very broad, but it’s also not deep; for most of us, it’s limited to voting in elections every few years, and in between these moments others make the decisions. The potential risk of this arrangement, as has been noted by astute observers since the birth of modern republics, is that citizens might grow distrustful of the people who are actually running government on a daily basis and of the special influences to which they might be subject. One way to address the problem of scale is to delegate much more power to states, provinces and localities. But on crucial issues of foreign trade, diplomacy or pressing constitutional questions, it’s impractical for individual states, regions or provinces to set their own policy. If large scale has the potential to lead to distrust and disengagement in a democracy, then a closely related problem is that of polarisation, which can take many forms, such as that involving tensions between different classes of people in the same location, or a difference of opinions between people living in different locations.
The absence of a state bureaucracy was a chief reason why early democracy proved to be such a stable form of rule for so many societies. With little autonomous power - apart from the ability to persuade - those who would have liked to rule as autocrats found themselves without the means to do so. The flipside of this was that, in many early democracies, those who were unhappy with a central decision could simply refuse to participate or even decamp to a new locality. Modern democracy lacks the same protections from central power that early democracies enjoyed. At the same time, having a powerful central state can allow a society to achieve goals such as universal education and prosperity, to name but a few. The question then is how to live with a state while preserving democracy.
Read the passage carefully and answer the following questions:
We must dispense with the idea that democracy is like a torch that gets passed from one leading society to another. The core feature of democracy - that those who rule can do so only with the consent of the people - wasn’t invented in one place at one time: it evolved independently in a great many human societies. Over several millennia and across multiple continents, early democracy was an institution in which rulers governed jointly with councils and assemblies of the people. Classical Greece provided particularly important instances of this democratic practice, and it’s true that the Greeks gave us a language for thinking about democracy, including the word demokratia itself. But they didn’t invent the practice. The core feature of early democracy was that the people had power, even if multiparty elections didn’t happen. The people, or at least some significant fraction of them, exercised this power in many different ways. In some cases, a ruler was chosen by a council or assembly, and was limited to being first among equals. In other instances, a ruler inherited their position, but faced constraints to seek consent from the people before taking actions both large and small.
The first difference between early democracy and our democracies today is that this earlier form of rule was a small-scale phenomenon. In Classical Athens those who had the right to participate in politics tended to do so in a very direct and intensive way, particularly in local assemblies. In modern democracy, participation is very broad, but it’s also not deep; for most of us, it’s limited to voting in elections every few years, and in between these moments others make the decisions. The potential risk of this arrangement, as has been noted by astute observers since the birth of modern republics, is that citizens might grow distrustful of the people who are actually running government on a daily basis and of the special influences to which they might be subject. One way to address the problem of scale is to delegate much more power to states, provinces and localities. But on crucial issues of foreign trade, diplomacy or pressing constitutional questions, it’s impractical for individual states, regions or provinces to set their own policy. If large scale has the potential to lead to distrust and disengagement in a democracy, then a closely related problem is that of polarisation, which can take many forms, such as that involving tensions between different classes of people in the same location, or a difference of opinions between people living in different locations.
The absence of a state bureaucracy was a chief reason why early democracy proved to be such a stable form of rule for so many societies. With little autonomous power - apart from the ability to persuade - those who would have liked to rule as autocrats found themselves without the means to do so. The flipside of this was that, in many early democracies, those who were unhappy with a central decision could simply refuse to participate or even decamp to a new locality. Modern democracy lacks the same protections from central power that early democracies enjoyed. At the same time, having a powerful central state can allow a society to achieve goals such as universal education and prosperity, to name but a few. The question then is how to live with a state while preserving democracy.
Which of the following cannot be inferred from the passage?
I. Classical Greece did not just invent the practice of democracy, but also gave us the word 'demokratia'.
II. The advantage of early democracies over modern ones is the very direct and intensive participation of the people in local assemblies.
III. The presence or absence of state bureaucracy is a vital factor affecting the stability of a democratic rule.
Read the passage carefully and answer the following questions:
Green energy investment is hot again in the U.S. To some, the new boom will raise the specter of the clean-tech bust that followed a streak of exuberance a decade ago. But there are reasons to believe that this time the trend is no bubble or mirage.
The most basic reason is that the fundamental underlying technology has matured in a way it simply hadn’t a decade ago. In 2009, the levelized cost of solar photovoltaic electricity was $359 per megawatt-hour — more than four times as expensive as electricity from a natural gas plant. By 2019, solar PV had fallen in price to $40 per megawatt-hour, 28% cheaper than gas. That’s an 89% decline in 10 years, with more cost drops yet to come. Meanwhile, lithium-ion batteries have experienced a similar drop in prices.
That order-of-magnitude drop in costs makes all the difference. First of all, it means that solar and wind aren’t risky new technologies. Solyndra, a solar manufacturer, failed in 2011 because it was trying to market an innovative new kind of solar cell, which ended up being too expensive when the tried-and-true design came down in cost. Future investments in solar won’t have to bet on any difficult technological breakthroughs. Batteries might be a different story — lots of money is being thrown at startups trying to create solid-state batteries, which would be a true breakthrough. But Tesla Inc. is doing just fine with the old kind, so that sector is probably going to do OK as well. Venture investing does well when it doesn’t have to bet on “hard tech”, and much of clean tech is no longer hard.
Second, cost drops in clean energy mean that success doesn’t depend on government intervention. In the earlier boom, fickle government subsidies were often necessary for capital-intensive energy companies to succeed. Now, even though President Joe Biden is planning a big push into clean-energy investment, the market is investing quite a lot in renewables all on its own.
Finally, investors have probably learned their lesson. Clean energy itself was never a good fit for venture. It’s capital intensive, since buying solar panels and wind turbines entails a lot of money up front; venture capital tends to focus on cheap, small investments that scale. And instead of companies creating highly differentiated products and new markets, as in software, clean electricity companies are basically all trying to provide the same commodified product.
This time around, venture capitalists are letting bigger investors handle the build out of solar and wind, and finding other niches where low-cost, differentiated startups can add value — such as solar services and financing, lab-grown meat and electric vehicles. Some of those bets are certainly going to fail, but that’s always the case in private equity. The success of Tesla — now with a market cap of almost $700 billion, or 28 times the amount that was lost in the clean-tech bust — demonstrates the time-honored principle that a few big hits can compensate for a lot of little failures.
In other words, clean tech is entering the final stage of the famous Gartner Hype Cycle — a pattern that describes the progression of emerging technologies and business models, starting with an innovation that sees expectations climb and then crash, before they finally rise again to sustained productivity. The clean-tech bust, like the dot-com bust in 2000, was a case of investor enthusiasm for a new technology outstripping the technology itself. But just as few today would question the value of companies like Google and Facebook that came into their own during a trough in investor enthusiasm, eventually the value of clean technology won’t be in question.
The central idea of the passage is that
Read the passage carefully and answer the following questions:
Green energy investment is hot again in the U.S. To some, the new boom will raise the specter of the clean-tech bust that followed a streak of exuberance a decade ago. But there are reasons to believe that this time the trend is no bubble or mirage.
The most basic reason is that the fundamental underlying technology has matured in a way it simply hadn’t a decade ago. In 2009, the levelized cost of solar photovoltaic electricity was $359 per megawatt-hour — more than four times as expensive as electricity from a natural gas plant. By 2019, solar PV had fallen in price to $40 per megawatt-hour, 28% cheaper than gas. That’s an 89% decline in 10 years, with more cost drops yet to come. Meanwhile, lithium-ion batteries have experienced a similar drop in prices.
That order-of-magnitude drop in costs makes all the difference. First of all, it means that solar and wind aren’t risky new technologies. Solyndra, a solar manufacturer, failed in 2011 because it was trying to market an innovative new kind of solar cell, which ended up being too expensive when the tried-and-true design came down in cost. Future investments in solar won’t have to bet on any difficult technological breakthroughs. Batteries might be a different story — lots of money is being thrown at startups trying to create solid-state batteries, which would be a true breakthrough. But Tesla Inc. is doing just fine with the old kind, so that sector is probably going to do OK as well. Venture investing does well when it doesn’t have to bet on “hard tech”, and much of clean tech is no longer hard.
Second, cost drops in clean energy mean that success doesn’t depend on government intervention. In the earlier boom, fickle government subsidies were often necessary for capital-intensive energy companies to succeed. Now, even though President Joe Biden is planning a big push into clean-energy investment, the market is investing quite a lot in renewables all on its own.
Finally, investors have probably learned their lesson. Clean energy itself was never a good fit for venture. It’s capital intensive, since buying solar panels and wind turbines entails a lot of money up front; venture capital tends to focus on cheap, small investments that scale. And instead of companies creating highly differentiated products and new markets, as in software, clean electricity companies are basically all trying to provide the same commodified product.
This time around, venture capitalists are letting bigger investors handle the build out of solar and wind, and finding other niches where low-cost, differentiated startups can add value — such as solar services and financing, lab-grown meat and electric vehicles. Some of those bets are certainly going to fail, but that’s always the case in private equity. The success of Tesla — now with a market cap of almost $700 billion, or 28 times the amount that was lost in the clean-tech bust — demonstrates the time-honored principle that a few big hits can compensate for a lot of little failures.
In other words, clean tech is entering the final stage of the famous Gartner Hype Cycle — a pattern that describes the progression of emerging technologies and business models, starting with an innovation that sees expectations climb and then crash, before they finally rise again to sustained productivity. The clean-tech bust, like the dot-com bust in 2000, was a case of investor enthusiasm for a new technology outstripping the technology itself. But just as few today would question the value of companies like Google and Facebook that came into their own during a trough in investor enthusiasm, eventually the value of clean technology won’t be in question.
The author compares the clean-tech bust to the dot-com bust because
Read the passage carefully and answer the following questions:
Green energy investment is hot again in the U.S. To some, the new boom will raise the specter of the clean-tech bust that followed a streak of exuberance a decade ago. But there are reasons to believe that this time the trend is no bubble or mirage.
The most basic reason is that the fundamental underlying technology has matured in a way it simply hadn’t a decade ago. In 2009, the levelized cost of solar photovoltaic electricity was $359 per megawatt-hour — more than four times as expensive as electricity from a natural gas plant. By 2019, solar PV had fallen in price to $40 per megawatt-hour, 28% cheaper than gas. That’s an 89% decline in 10 years, with more cost drops yet to come. Meanwhile, lithium-ion batteries have experienced a similar drop in prices.
That order-of-magnitude drop in costs makes all the difference. First of all, it means that solar and wind aren’t risky new technologies. Solyndra, a solar manufacturer, failed in 2011 because it was trying to market an innovative new kind of solar cell, which ended up being too expensive when the tried-and-true design came down in cost. Future investments in solar won’t have to bet on any difficult technological breakthroughs. Batteries might be a different story — lots of money is being thrown at startups trying to create solid-state batteries, which would be a true breakthrough. But Tesla Inc. is doing just fine with the old kind, so that sector is probably going to do OK as well. Venture investing does well when it doesn’t have to bet on “hard tech”, and much of clean tech is no longer hard.
Second, cost drops in clean energy mean that success doesn’t depend on government intervention. In the earlier boom, fickle government subsidies were often necessary for capital-intensive energy companies to succeed. Now, even though President Joe Biden is planning a big push into clean-energy investment, the market is investing quite a lot in renewables all on its own.
Finally, investors have probably learned their lesson. Clean energy itself was never a good fit for venture. It’s capital intensive, since buying solar panels and wind turbines entails a lot of money up front; venture capital tends to focus on cheap, small investments that scale. And instead of companies creating highly differentiated products and new markets, as in software, clean electricity companies are basically all trying to provide the same commodified product.
This time around, venture capitalists are letting bigger investors handle the build out of solar and wind, and finding other niches where low-cost, differentiated startups can add value — such as solar services and financing, lab-grown meat and electric vehicles. Some of those bets are certainly going to fail, but that’s always the case in private equity. The success of Tesla — now with a market cap of almost $700 billion, or 28 times the amount that was lost in the clean-tech bust — demonstrates the time-honored principle that a few big hits can compensate for a lot of little failures.
In other words, clean tech is entering the final stage of the famous Gartner Hype Cycle — a pattern that describes the progression of emerging technologies and business models, starting with an innovation that sees expectations climb and then crash, before they finally rise again to sustained productivity. The clean-tech bust, like the dot-com bust in 2000, was a case of investor enthusiasm for a new technology outstripping the technology itself. But just as few today would question the value of companies like Google and Facebook that came into their own during a trough in investor enthusiasm, eventually the value of clean technology won’t be in question.
According to the author, which of the following is NOT a feature of venture investing?
I. Venture investing generally thrives when the decisions are not contingent on technological breakthroughs.
II. Venture capitalists largely invest in low-risk endeavours.
III. Venture capitalists focus on cheap, small investments that are scalable.
IV. Venture capitalists do not invest in established technology companies that have achieved economies of scale.
Read the passage carefully and answer the following questions:
Over the last decade, an increasingly confident right wing has presented disillusioned voters with a simple choice: elitist, neoliberal hyper-globalisation or popular, patriotic nationalism. This new fault-line pits economic and social liberalism against social conservatism and the promise of muscular economic intervention. Despite the defeat of Donald Trump in 2020, progressives have yet to find a strategy to combat this potent—if false—divide.
The traditional right-left dividing line—economic liberalism and social conservatism on the right, economic interventionism and social liberalism on the left—forced working-class nationalists to choose between their socially conservative instincts (including hostility to immigration) and their support for state intervention in the economy. In essence, they had to decide which liberalism—social or economic—to reject.
The 2016 Brexit referendum freed such voters from this restraint—and it certainly set back the old liberal order. But despite many jumping to the conclusion that fervent nationalism explained the whole Brexit phenomenon, it was not clear which liberalism was being rejected. Many of the towns that repudiated the EU were voting just as much against the deindustrialisation that took place during the years Britain was in the EU as they were voting to restore a supposedly Edenic 1950s. Back in the conventional world of parliamentary elections, in 2017 Labour’s anti-neoliberal economic programme under Jeremy Corbyn added 3.5m votes to its 2015 general election tally. But by 2019, identity trumped economics—on which the Tories, Labour's opponents, had anyway begun to change their tune under Boris Johnson—and the red wall crumbled.
The British right was not alone in affecting to spurn both liberalisms. From Warsaw via Workington to Wisconsin, working-class voters received promises from right-wing populists that their economic interests would not be sacrificed on the altar of neoliberalism. Poland’s Law and Justice Party adopted an economic and social programme that would win over “left-behind” Poles. Marine Le Pen’s National Front professed to abandon its fascist past and moved the spotlight onto protecting French industry. Johnson committed his party to an interventionist “levelling-up” agenda. And Trump promised industrial protection against overseas competition, as well as the biggest programme of public works since the New Deal.
This new fault-line not only redrew the political map: it fractured the old consensus around core democratic values—stretching from right to left—that had existed since the Second World War. These values were rooted in the French Revolution and European Enlightenment and comprised an alliance of liberty, equality and solidarity, which could accommodate Christian Democrats, liberals, social democrats and orthodox socialists, albeit in different proportions.
The nationalist far-right rejects these values. Echoing the rhetorical tropes of anti-democratic forces from the interwar years, populists like Trump promote conspiracy theories in which liberal politicians plot to destroy national sovereignty in the interests of global financial capital. A politics of demonisation, exclusion and “othering” has seeped into mainstream right-wing parties. In the United States, it culminated in Trump’s incitement of his supporters to storm the Capitol on 6th January to overturn the result of the 2020 election.
In a recent essay, Timothy Garton Ash argues that “liberals need to join both conservatives and socialists in full-heartedly embracing the value of solidarity.” But for intellectual conservatives like the late Roger Scruton (whom Garton Ash quotes) as well as chauvinist politicians—like Trump, Le Pen, Viktor Orbán and the Italian League’s Matteo Salvini—solidarity always has to rely on an inherently exclusionary notion of identity: we’re who we are because you’re not. Progressive social solidarity is, by contrast, accepting of difference. However, socialists and liberals have much in common in the battle against the far right: together, they can build on the social gains of the Harold Wilson and Tony Blair governments, allying around social and political liberty as well as the economics of equality.
Which of the following statements can be inferred from the passage?
The passage given below is followed by four summaries. Choose the option that best captures the author’s position.
Language bias in academia is something that researchers have been facing for a long time. Not only are the vast majority of scientific papers published in English, the ‘correctness’ of English used in them is a factor that determines their acceptance into top journals—which, incidentally, also publish exclusively in English. It discourages non-English speaking researchers as it prioritizes the purity of the language over the content of their research. This also puts them at a disadvantage professionally, as they’re robbed of the most common, popular platforms that can further their research and careers. In addition, the overwhelming reliance on, and preference of, English favours only research that looks at the world in specific predisposed ways, brought on by the use of English, such as the tendency to prescribe indigenous knowledge as ‘folklore’ and not something that could have factual validity. It discounts anything that digresses from the norm, even when the information might be highly relevant and important.
Five sentences related to a topic are given below. Four of them can be put together to form a meaningful and coherent short paragraph. Identify the odd one out.
1. Gaura Devi led 27 of the village women to the site and confronted the loggers.
2. On 26 March 2018, a Chipko movement conservation initiative was marked by Google Doodle on its 45th anniversary.
3. On 25 March 1974, the day the lumbermen were to cut the trees, the men of Reni village and DGSS workers were in Chamoli, diverted by the state government and contractors to a fictional compensation payment site, while back home labourers arrived by the truckload to start logging operations.
4. When all talking failed, and the loggers started to shout and abuse the women, threatening them with guns, the women resorted to hugging the trees to stop them from being felled.
5. A local girl, on seeing them, rushed to inform Gaura Devi, the head of the village Mahila Mangal Dal, at Reni village.
The four sentences (labelled 1, 2, 3, and 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. However, such unbridled advancements have also escalated global issues like climate change, resource depletion, and significant socio-economic disparities.
2. The 21st century has been heralded as an era of technological marvels, transforming every facet of human life with unprecedented innovations.
3. These challenges necessitate a reconfiguration of global priorities towards sustainability and equitable progress, demanding collaborative, not isolated, innovation.
4. Consequently, the narrative of development has increasingly become a balancing act between embracing technological growth and acknowledging its consequential perils.
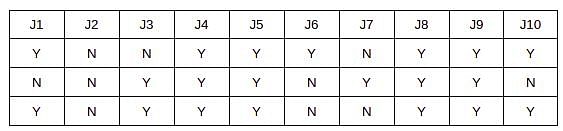
A lock is guarded by a security code that serves as the password. The code is in the following form:
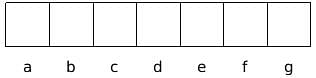
Where a, b, c, d and g are numbers and e, f are alphabets. The following information is also known about the respective characters:
1. 'a' is a prime number from 1 to 10.
2. The 2-digit number 'bc' is also a prime number such that b = a + 1.
3. 'd' = 'bc' % 'a', that is, d is the remainder when the 2-digit number 'bc' is divided by 'a'.
4. 'e' is the alphabet at the index of n, alphabet[n], where n is the highest number of occurrences of any digit(0 to 9) among a,b,c,d. Here,alphabet[1] = A, alphabet[2] = B,..., alphabet[26] = Z.
5. 'f' is the alphabet either preceding or succeeding the alphabet 'e' when all English alphabets are arranged alphabetically.
6. 'g' is the remainder when the sum of digits a, b, c and d is divided by 10. g = (a+b+c+d)%10.
Based on the information given above, answer the questions that follow.
If we consider all possible codes, how many distinct alphabets appear at least once in any of the codes?
A lock is guarded by a security code that serves as the password. The code is in the following form:
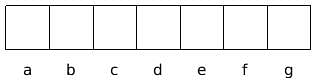
Where a, b, c, d and g are numbers and e, f are alphabets. The following information is also known about the respective characters:
1. 'a' is a prime number from 1 to 10.
2. The 2-digit number 'bc' is also a prime number such that b = a + 1.
3. 'd' = 'bc' % 'a', that is, d is the remainder when the 2-digit number 'bc' is divided by 'a'.
4. 'e' is the alphabet at the index of n, alphabet[n], where n is the highest number of occurrences of any digit(0 to 9) among a,b,c,d. Here,alphabet[1] = A, alphabet[2] = B,..., alphabet[26] = Z.
5. 'f' is the alphabet either preceding or succeeding the alphabet 'e' when all English alphabets are arranged alphabetically.
6. 'g' is the remainder when the sum of digits a, b, c and d is divided by 10. g = (a+b+c+d)%10.
Based on the information given above, answer the questions that follow.
How many codes are possible?
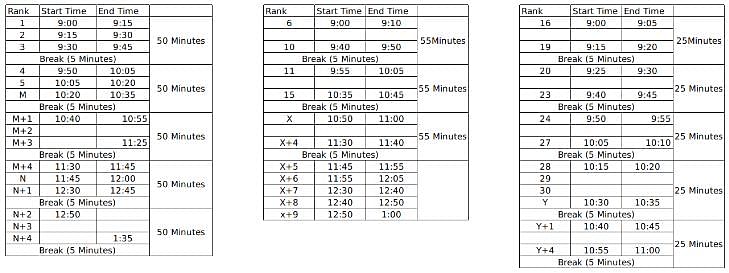
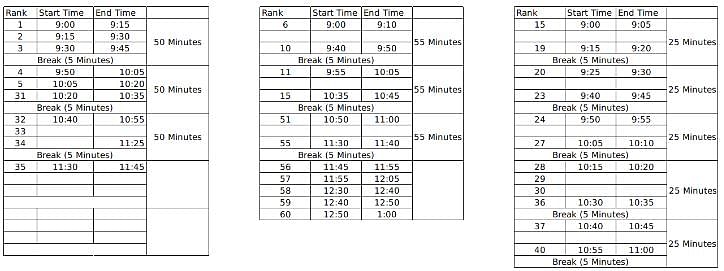
60 students were shortlisted for their Personal Interview by the Indian School of Management. But the interview process was to be conducted online and hence students were sent the KOOM meeting link for the same. All the 60 students were to join the KOOM common room at 9:00 AM sharp and then the admission co-ordinators would send in a certain number of students to different waiting rooms- X, Y and Z prior to their one on one interviews with the panellists. There were 3 panellists- A, B and C who were conducting interviews for the candidates waiting in the rooms X, Y and Z respectively. The capacity for the waiting rooms X, Y and Z were 5, 10 and 15 respectively.
The 60 students were given a rank from 1 to 60 based on their composite score and it is known that no two students got the same score. To start off the interviews, the ones with top 5 ranks are sent to panellist A. The 10 below them are sent to B and students ranked 16 to 30 were sent to C. When the last person from the waiting room X, Y and Z gives an interview, the next set of students are immediately sent to the waiting room as soon as the interview gets over and the priority is maintained as students with higher ranks are sent to X, Y and Z respectively if the interviews of the previous batch end simultaneously.
It is known that:
1. Panellist A takes an interview for 15 minutes and takes a break of 5 minutes only after interviewing 3 candidates
2. Panellist B takes an interview for 10 minutes and takes a break of 5 minutes after interviewing 5 students.
3. Panellist C takes an interview of 5 minutes and takes a break of 5 minutes after interviewing 4 students.
4. Lunch break is scheduled between 12:00 noon to 12:30 PM and students are not cut abruptly if their interview began before 12:00 noon, i.e. the interviewers take the break only after finishing the interview if it started before 12:00 noon.
5. Batches of 5, 10 and 15 students enter the waiting room together such that students who enter the waiting room at a time have continuous ranks. For example, if the interviewer X is ending up the interview of the last student from the previous batch, 5 students with continuous ranks (say 21-25) enter the waiting room X together.
6. Students allotted to a particular waiting room is only interviewed by the designated interviewer and is not interviewed by anyone else even if the other interviewer is free.
7. If panellist A goes into the lunch break after having interviewed 1 student, he will again take his 5 minute break after interviewing 2 students post the lunch break so as to satisfy the condition 1 always. The same applies for panellist B and C who follow conditions 2 and 3 respectively.
When does interviewer B finish his last interview?
60 students were shortlisted for their Personal Interview by the Indian School of Management. But the interview process was to be conducted online and hence students were sent the KOOM meeting link for the same. All the 60 students were to join the KOOM common room at 9:00 AM sharp and then the admission co-ordinators would send in a certain number of students to different waiting rooms- X, Y and Z prior to their one on one interviews with the panellists. There were 3 panellists- A, B and C who were conducting interviews for the candidates waiting in the rooms X, Y and Z respectively. The capacity for the waiting rooms X, Y and Z were 5, 10 and 15 respectively.
The 60 students were given a rank from 1 to 60 based on their composite score and it is known that no two students got the same score. To start off the interviews, the ones with top 5 ranks are sent to panellist A. The 10 below them are sent to B and students ranked 16 to 30 were sent to C. When the last person from the waiting room X, Y and Z gives an interview, the next set of students are immediately sent to the waiting room as soon as the interview gets over and the priority is maintained as students with higher ranks are sent to X, Y and Z respectively if the interviews of the previous batch end simultaneously.
It is known that:
1. Panellist A takes an interview for 15 minutes and takes a break of 5 minutes only after interviewing 3 candidates
2. Panellist B takes an interview for 10 minutes and takes a break of 5 minutes after interviewing 5 students.
3. Panellist C takes an interview of 5 minutes and takes a break of 5 minutes after interviewing 4 students.
4. Lunch break is scheduled between 12:00 noon to 12:30 PM and students are not cut abruptly if their interview began before 12:00 noon, i.e. the interviewers take the break only after finishing the interview if it started before 12:00 noon.
5. Batches of 5, 10 and 15 students enter the waiting room together such that students who enter the waiting room at a time have continuous ranks. For example, if the interviewer X is ending up the interview of the last student from the previous batch, 5 students with continuous ranks (say 21-25) enter the waiting room X together.
6. Students allotted to a particular waiting room is only interviewed by the designated interviewer and is not interviewed by anyone else even if the other interviewer is free.
7. If panellist A goes into the lunch break after having interviewed 1 student, he will again take his 5 minute break after interviewing 2 students post the lunch break so as to satisfy the condition 1 always. The same applies for panellist B and C who follow conditions 2 and 3 respectively.
When was the interview of the student ranked 53 finished?
60 students were shortlisted for their Personal Interview by the Indian School of Management. But the interview process was to be conducted online and hence students were sent the KOOM meeting link for the same. All the 60 students were to join the KOOM common room at 9:00 AM sharp and then the admission co-ordinators would send in a certain number of students to different waiting rooms- X, Y and Z prior to their one on one interviews with the panellists. There were 3 panellists- A, B and C who were conducting interviews for the candidates waiting in the rooms X, Y and Z respectively. The capacity for the waiting rooms X, Y and Z were 5, 10 and 15 respectively.
The 60 students were given a rank from 1 to 60 based on their composite score and it is known that no two students got the same score. To start off the interviews, the ones with top 5 ranks are sent to panellist A. The 10 below them are sent to B and students ranked 16 to 30 were sent to C. When the last person from the waiting room X, Y and Z gives an interview, the next set of students are immediately sent to the waiting room as soon as the interview gets over and the priority is maintained as students with higher ranks are sent to X, Y and Z respectively if the interviews of the previous batch end simultaneously.
It is known that:
1. Panellist A takes an interview for 15 minutes and takes a break of 5 minutes only after interviewing 3 candidates
2. Panellist B takes an interview for 10 minutes and takes a break of 5 minutes after interviewing 5 students.
3. Panellist C takes an interview of 5 minutes and takes a break of 5 minutes after interviewing 4 students.
4. Lunch break is scheduled between 12:00 noon to 12:30 PM and students are not cut abruptly if their interview began before 12:00 noon, i.e. the interviewers take the break only after finishing the interview if it started before 12:00 noon.
5. Batches of 5, 10 and 15 students enter the waiting room together such that students who enter the waiting room at a time have continuous ranks. For example, if the interviewer X is ending up the interview of the last student from the previous batch, 5 students with continuous ranks (say 21-25) enter the waiting room X together.
6. Students allotted to a particular waiting room is only interviewed by the designated interviewer and is not interviewed by anyone else even if the other interviewer is free.
7. If panellist A goes into the lunch break after having interviewed 1 student, he will again take his 5 minute break after interviewing 2 students post the lunch break so as to satisfy the condition 1 always. The same applies for panellist B and C who follow conditions 2 and 3 respectively.
When did the 50th ranked student finish his/her interview?
60 students were shortlisted for their Personal Interview by the Indian School of Management. But the interview process was to be conducted online and hence students were sent the KOOM meeting link for the same. All the 60 students were to join the KOOM common room at 9:00 AM sharp and then the admission co-ordinators would send in a certain number of students to different waiting rooms- X, Y and Z prior to their one on one interviews with the panellists. There were 3 panellists- A, B and C who were conducting interviews for the candidates waiting in the rooms X, Y and Z respectively. The capacity for the waiting rooms X, Y and Z were 5, 10 and 15 respectively.
The 60 students were given a rank from 1 to 60 based on their composite score and it is known that no two students got the same score. To start off the interviews, the ones with top 5 ranks are sent to panellist A. The 10 below them are sent to B and students ranked 16 to 30 were sent to C. When the last person from the waiting room X, Y and Z gives an interview, the next set of students are immediately sent to the waiting room as soon as the interview gets over and the priority is maintained as students with higher ranks are sent to X, Y and Z respectively if the interviews of the previous batch end simultaneously.
It is known that:
1. Panellist A takes an interview for 15 minutes and takes a break of 5 minutes only after interviewing 3 candidates
2. Panellist B takes an interview for 10 minutes and takes a break of 5 minutes after interviewing 5 students.
3. Panellist C takes an interview of 5 minutes and takes a break of 5 minutes after interviewing 4 students.
4. Lunch break is scheduled between 12:00 noon to 12:30 PM and students are not cut abruptly if their interview began before 12:00 noon, i.e. the interviewers take the break only after finishing the interview if it started before 12:00 noon.
5. Batches of 5, 10 and 15 students enter the waiting room together such that students who enter the waiting room at a time have continuous ranks. For example, if the interviewer X is ending up the interview of the last student from the previous batch, 5 students with continuous ranks (say 21-25) enter the waiting room X together.
6. Students allotted to a particular waiting room is only interviewed by the designated interviewer and is not interviewed by anyone else even if the other interviewer is free.
7. If panellist A goes into the lunch break after having interviewed 1 student, he will again take his 5 minute break after interviewing 2 students post the lunch break so as to satisfy the condition 1 always. The same applies for panellist B and C who follow conditions 2 and 3 respectively.
At what time does Interviewer A finish all his interviews?
5 persons- P1, P2, P3, P4 and P5 took part in a unique high jump competition where each one was given 10 chances to maximise their points. Each one of them started with a height of 150 cm to clear. If a particular participant cleared the height, in the next jump he was to clear a height of 5 cm more than the previous one. For eg. if a participant cleared 150 cm in his first jump, he will need to clear the height of 155 cm in his next jump. A foul is said to be committed if the participant fails to clear the barrier height. 3 continuous fouls would lead to straight elimination. 10 points are given to a participant who clears the given height and 2 points are deducted for every foul. Also, a participant is said to face an elimination jump if he had committed fouls on both of his two previous attempts. The following additional information is known about the jumps made by the 5 participants-
1. P5 was eliminated in his 5th jump and managed to score a total of points in single digit.
2. P1 and P2 faced elimination jumps thrice but managed to escape elimination. P1 never cleared two jumps continuously without a foul but P2 did this exactly once. Both of them scored 28 points each and cleared the 10th jump.
3. P4 was the only participant who made a maximum of 3 jumps continuously twice and he faced elimination jump once and escaped elimination.
4. P3 was eliminated in his 8th jump and he never faced the elimination jump before his 8th jump. Also, he cleared two different heights in two jumps continuously exactly once.
5. P2 failed in his 4th and 7th jumps.
6. P4 made a foul in his second jump.
How many participants did not commit a foul in their 5th attempt?
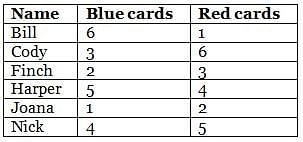
Directions: Read the passage and answer the following question.
Bill, Cody, Finch, Harper, Joana and Nick are playing a card game which had blue and red coloured cards. At the end of the game, each person was left with each of the two colored cards ranging from 1 to 6 in number.
No two persons have the same number of cards of the same colour.
Further, it is also known that:
(1) For any person, the sum of the number of cards with that person in both the colours is an odd number.
(2) Cody had more blue cards than Finch.
(3) The difference in the number of blue cards of Bill and red cards of Harper is 2.
(4) Finch, who has three red cards, has less blue cards than at least three persons.
(5) Harper, who has more blue cards than at least three persons, has more red cards than Joana.
(6) Nick has four blue cards and more red cards than those with Harper.
Q. How many blue cards are there with Cody?
Directions: Read the passage and answer the following question.
Bill, Cody, Finch, Harper, Joana and Nick are playing a card game which had blue and red coloured cards. At the end of the game, each person was left with each of the two colored cards ranging from 1 to 6 in number.
No two persons have the same number of cards of the same colour.
Further, it is also known that:
(1) For any person, the sum of the number of cards with that person in both the colours is an odd number.
(2) Cody had more blue cards than Finch.
(3) The difference in the number of blue cards of Bill and red cards of Harper is 2.
(4) Finch, who has three red cards, has less blue cards than at least three persons.
(5) Harper, who has more blue cards than at least three persons, has more red cards than Joana.
(6) Nick has four blue cards and more red cards than those with Harper.
Q. How many people have less cards than Harper in both blue and red colours?
Directions: Read the passage and answer the following question.
Bill, Cody, Finch, Harper, Joana and Nick are playing a card game which had blue and red coloured cards. At the end of the game, each person was left with each of the two colored cards ranging from 1 to 6 in number.
No two persons have the same number of cards of the same colour.
Further, it is also known that:
(1) For any person, the sum of the number of cards with that person in both the colours is an odd number.
(2) Cody had more blue cards than Finch.
(3) The difference in the number of blue cards of Bill and red cards of Harper is 2.
(4) Finch, who has three red cards, has less blue cards than at least three persons.
(5) Harper, who has more blue cards than at least three persons, has more red cards than Joana.
(6) Nick has four blue cards and more red cards than those with Harper.
Q. Who has the same number of blue cards as the number of red cards with Bill?
Directions: Read the passage and answer the following question.
Bill, Cody, Finch, Harper, Joana and Nick are playing a card game which had blue and red coloured cards. At the end of the game, each person was left with each of the two colored cards ranging from 1 to 6 in number.
No two persons have the same number of cards of the same colour.
Further, it is also known that:
(1) For any person, the sum of the number of cards with that person in both the colours is an odd number.
(2) Cody had more blue cards than Finch.
(3) The difference in the number of blue cards of Bill and red cards of Harper is 2.
(4) Finch, who has three red cards, has less blue cards than at least three persons.
(5) Harper, who has more blue cards than at least three persons, has more red cards than Joana.
(6) Nick has four blue cards and more red cards than those with Harper.
Q. How many red cards more/less does Harper have than Bill? Key in the number.
C-Biz is a network marketing platform wherein a pyramid scheme is followed. The member who joins initially gets 25% of the revenue generated as commission. He is also liable to get an additional 25% of the commissions generated by a member who was referred by him. And this scheme goes on till infinity. If the revenue generated by each of the members of C-Biz is Rs. 20,000; then what amount is earned by the first member who referred another member only once, who in turn referred another only once and so on?
What is the number of integers in the domain of (15−2x) C (x+3) ?
Grapes when dried up turn into raisins. A raisin has only 5% of water and grapes have 80% of water. 2 faulty weighing machines- A and B are used to measure grapes and raisins respectively. Faulty weighing machine A shows 10% less weight than the correct weight and faulty weighing machine B shows 10% more weight than the correct weight. A certain amount of grapes and raisins was measured, and according to the readings displayed by the balances, the mixture had 20% water content. What approximately was the true water content of the mixture of raisins and grapes that were measured?
A city is classified as a green city when its forest cover is greater than or equal to 20%. The mayor of Hyderabad wanted the city to fall under this category. When calculated, it was seen that the forest area cannot increase by more than 4% annually. If the current forest area of Hyderabad is 17%, then after 'x' years, Hyderabad falls under the category of Green city, where x is the smallest possible integer. Then x=?
A right-angled triangle ABC has an inradius and circumradius of 4 cm and 10 cm respectively. What is the area of triangle ABC in sq. cm?
If A, B, C and D are distinct natural numbers, the sum of which adds up to 50. Then, the maximum value of their product is __?
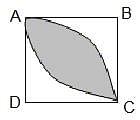
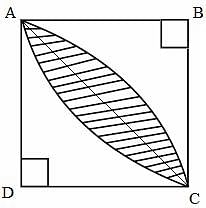
In the diagram, square ABCD has a side length of 6 units. Circular arcs of radius 6 units are drawn with centres B and D. What is the area of the shaded region?
Alok took a loan of Rs. 24000 at 5% simple interest per annum from Bhanu. He immediately lent out one-third of the money to Clara at 4% compound interest for two years and the rest to Dhruv at 8% simple interest. How much did Alok earn (in rupees) from the entire transactions if the money was returned back by Clara and Dhruv at the end of the second year? Consider Alok paying back the loan to Bhanu as soon as he got the money back from the other two.
|
152 docs|327 tests
|



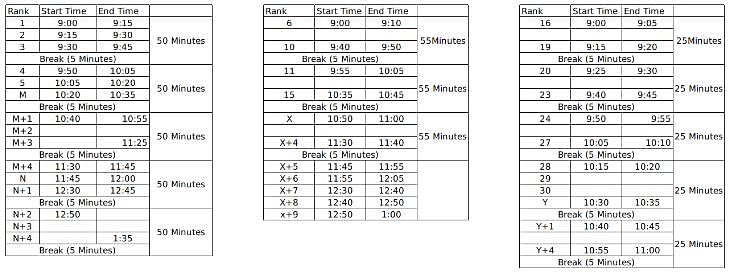
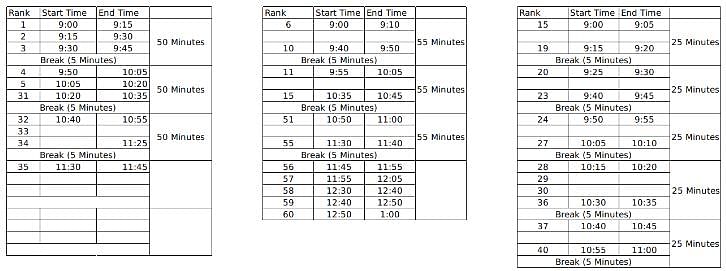
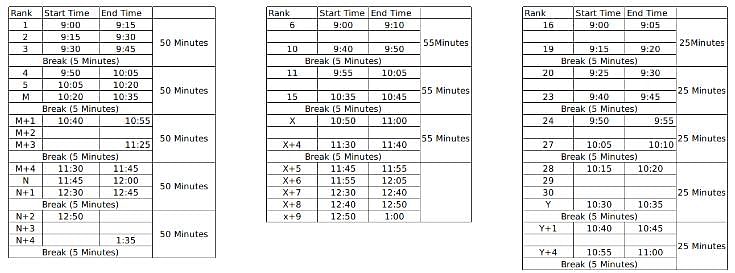
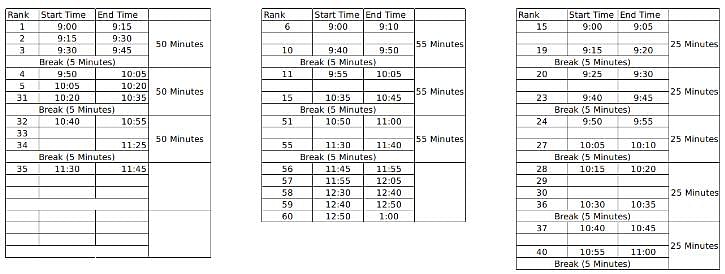
 Here, M, N, X and Y are the ranks of the students. M to M+4 are the set of 5 students who will be interviewed once the interview of the student ranked 5th gets over and similarly for others.
Here, M, N, X and Y are the ranks of the students. M to M+4 are the set of 5 students who will be interviewed once the interview of the student ranked 5th gets over and similarly for others.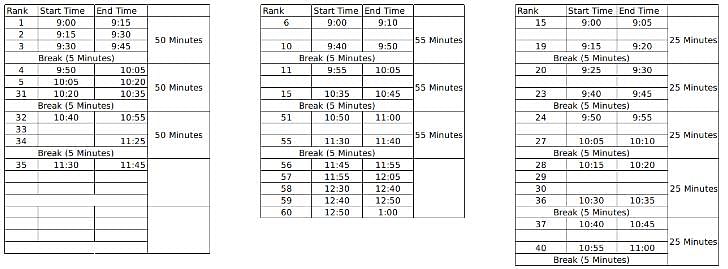









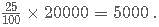
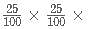

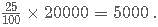
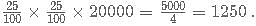

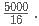
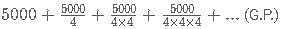

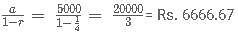

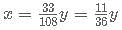
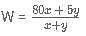
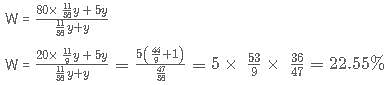
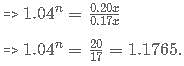
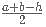
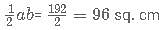
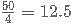
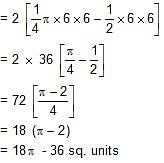
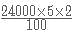 = 24000+2400= Rs. 26,400.
= 24000+2400= Rs. 26,400.
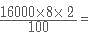 = 16000+2560= Rs. 18560.
= 16000+2560= Rs. 18560.














