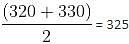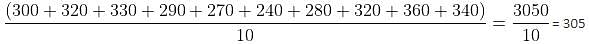CAT Mock Test- 7 - CAT MCQ
30 Questions MCQ Test CAT Mock Test Series 2024 - CAT Mock Test- 7
All of the following options represent causes reflective of effective altruism EXCEPT:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The passage makes all of the following claims about effective altruism, EXCEPT
According to the author, the efficiency view promoted by effective altruism
In the third paragraph, why does the author remark that "ironically, the roles have reversed?"?
According to the author, what was the reason for the shift toward the fear of chaotic human behavior?
The risk in Wiener's distinction between what we desire and what actually happens, in the end, is that:
Which of the following could be an example of Weiner's desire-outcome disparity argument?
I. A weapons system, which cannot be stopped easily, starts bombing after receiving an erroneous command.
II. An AI program developed to mitigate global warming starts eliminating a fraction of the human population to complete its objective.
III. A Social media platform allows groups of militants to communicate their plans and coordinate their attacks.
Which of the following statements CANNOT be inferred from the passage concerning the Nordic regions?
I. Progressive policies have not addressed the presence of gender stereotypes in the workplace.
II. Competition among women has exacerbated the income gap between men and women.
III. Occupational gender segregation has led to segregation in education on major subjects.
IV. Social norms discourage women from taking up certain occupations.
All of the following have been discussed about gender equality in Sweden, EXCEPT:
Which of the following is likely to be the next course of discussion?
Which of the following cannot be inferred?
I. The effectiveness of 'big data' is determined not by its size but by its diversity.
II. Genes are a major factor influencing autism.
III. Consumption of a diet containing low levels of phenylalanine helps decrease the level of amino acid in the blood.
All of the following have been discussed in the passage as benefits of having richer and bigger datasets EXCEPT:
The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. On the contrary, the industry is happy reducing the wage bills, doing mechanisation and raising its profits.
2. During the pandemic, nearly 31 million families have moved down from the middle class and nearly 100 million people have lost jobs.
3. The industries that are most likely to create employment, i.e. the medium and small industries, are going down under and the large ones which do not create employment are the poster boys.
4. They are the ones that will get the 6 per cent productivity-linked incentive from the tax paid by the average taxpayers, with unknown consequences.
The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. For others, Trump’s loss makes him into a loser—especially damaging given how much Trump hates losers.
2. In the more immediate future, however, no one will remain as personally angry about it as Trump.
3. Polls show that many Republicans believe the 2020 election was tainted, and the damage that will do to faith in democracy in the long term is dangerous.
4. Some followers who saw him as a man who could challenge the establishment will view his defeat as proof that politics is irredeemable, and will slide into apathy and disengagement.
Five sentences related to a topic are given below. Four of them can be put together to form a meaningful and coherent short paragraph. Identify the odd one out.
1. Without robust national privacy safeguards, entire databases of citizen information are ready for purchase, whether to predatory loan companies, law enforcement agencies, or even malicious foreign actors.
2. Federal privacy bills that don’t give sufficient attention to data brokerage will therefore fail to tackle an enormous portion of the data surveillance economy.
3. Data brokerage is a threat to democracy.
4. This is why the largest data brokers are lobbying more aggressively in Washington.
5. This will leave civil rights, national security, and public-private boundaries vulnerable in the process.
Five sentences related to a topic are given below. Four of them can be put together to form a meaningful and coherent short paragraph. Identify the odd one out.
1. Researchers see signs of this in sperm whales in the Galápagos and the Caribbean, in humpbacks across the South Pacific, in Arctic belugas, and in the Pacific Northwest’s killer whales.
2. Today many scientists believe some whales and dolphins, like humans, have distinct cultures.
3. Whale culture, it seems, is rattling timeworn conceptions of ourselves.
4. The possibility is prompting new thinking about how some marine species evolve.
5. Cultural traditions may help drive genetic shifts, altering what it means to be a whale.
The four sentences (labelled 1, 2, 3, and 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. However, the very ubiquity of such technology poses critical questions about data privacy and individual autonomy.
2. The integration of advanced algorithms and everyday technology has streamlined countless processes, improving efficiency exponentially.
3. As we entrust more of our lives to digital gatekeepers, the parameters of the debates shift from technical concerns to ethical dilemmas.
4. Such an environment, teeming with both subtle surveillance and convenience, highlights the double-edged nature of progress.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Urban biodiversity plays a crucial role in enhancing city residents' quality of life. It aids in pollution reduction, provides psychological benefits, and helps regulate urban temperatures. Despite its importance, urban biodiversity is often overlooked in city planning, with priority given to industrial and residential development. This neglect can lead to the degradation of local ecosystems and loss of species, potentially triggering broader environmental consequences. Integrating green spaces and biodiversity considerations into urban development plans is imperative for sustainable city living.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
The surge in freelance and gig-based employment is reshaping the traditional work environment. While offering flexibility and autonomy, the gig economy also ushers in challenges such as job insecurity, lack of benefits, and an inconsistent income stream. Governments struggle to catch up with this evolving employment model, often leaving workers unprotected under labor laws. Moving forward requires reimagining labor policies to provide gig workers with adequate security and rights, ensuring a fair work environment.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Modern dietary patterns, driven by a quest for convenience and speed, have led to an increase in processed food consumption and a decline in nutritional quality. This shift contributes to various health issues, including obesity, diabetes, and heart disease, straining healthcare systems globally. Public health initiatives emphasize returning to whole foods and balanced diets, but this change is hindered by advertising, fast-paced lifestyles, and food deserts. Addressing these challenges requires comprehensive strategies that include public education, improved food policies, and collaboration with food producers for healthier options.
Directions: Read the question carefully and answer the question that follows:
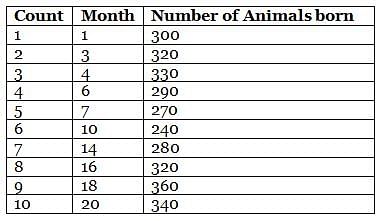
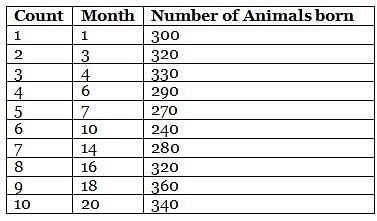
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. What is the average number of animals born between second count and third count that Mr. Wilson counted?
Directions: Read the question carefully and answer the question that follows:
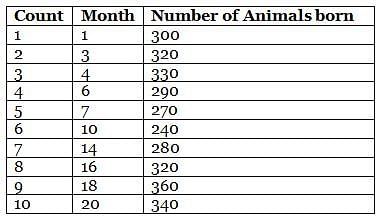
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. What is the difference between the fifth count and the ninth count that Mr. Wilson took?
Directions: Read the question carefully and answer the question that follows:
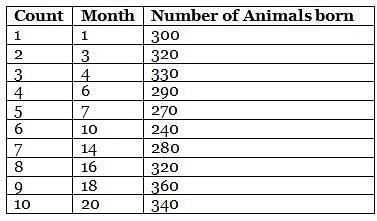
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. On which of the following months did Mr. Wilson count the number of animals born?
Directions: Read the question carefully and answer the question that follows:
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. What is the average of the number of animals born during the ten months that Mr. Wilson counted?
Directions: Read the question carefully and answer the question that follows:
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. How many months had elapsed before Mr. Wilson began his fourth count? Key in the value.
Directions: Refer to the illustrations below and answer the question that follows.

Total units sold in 2014 = 2,52,000
Total units sold in 2015 = 3,24,000
Percent defective units of total units sold for each product:

Q. How many defective units of product A were sold in 2014 and 2015?
|
16 videos|27 docs|58 tests
|
|
16 videos|27 docs|58 tests
|