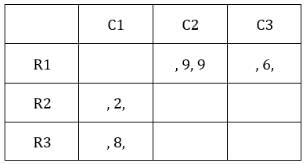
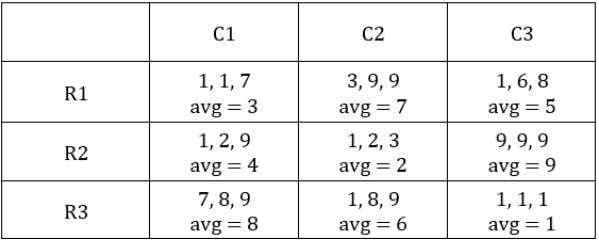
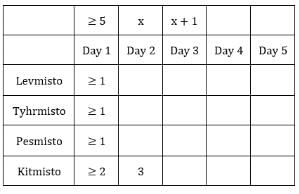
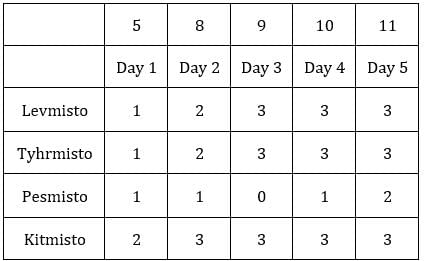
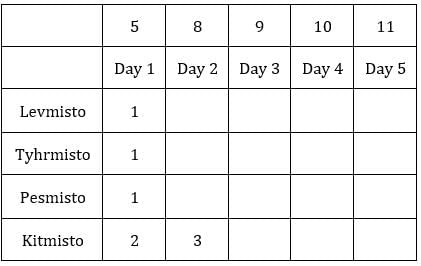
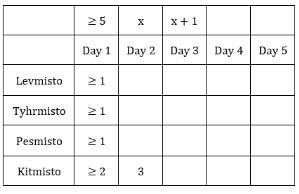
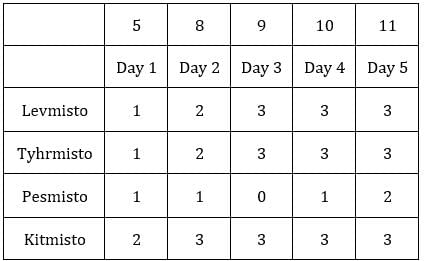
Each box has three sacks. We will consider three values for each sacks representing the number of coins in each sack in ascending order.
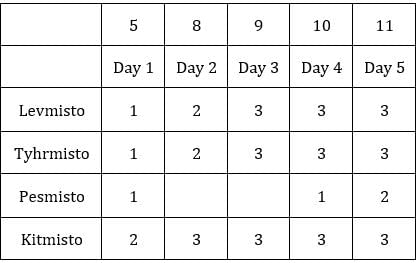
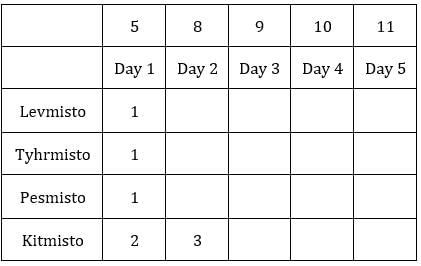
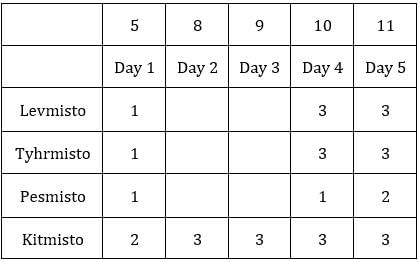
Table 1: Medians of C1R2, C1R3, C2R1 and C3R1 are given. If numbers of coins in each sack is written in ascending order for all boxes, these medians will be the middle value.
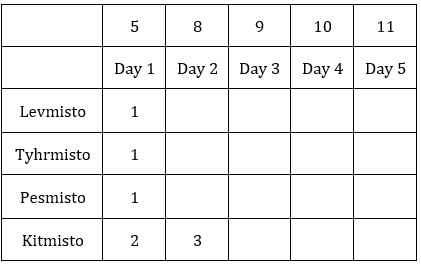
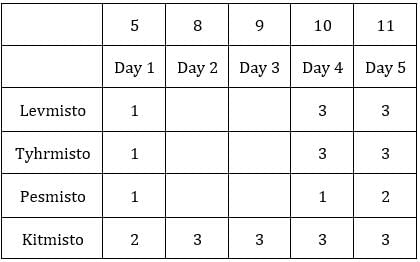
Median for C2R1 is 9, hence the third value must be 9.
Table 2:
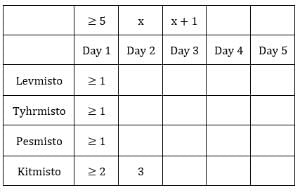
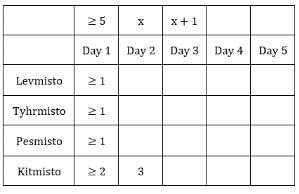
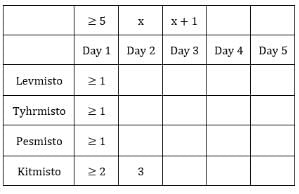
The number given represents the number of sacks having more than 5 coins. We can represent this information as follows:

C2R1: The sum of coins so far is 9 + 9 = 18.
*Exactly one condition is satisfied i.e., highest number coins in a sack is 9.
The first sack should have coins less than 5 and the average should be an integer.
This is possible only when the first sack has 3 coins.
∴ Average number of coins/sack = (3 + 9 + 9)/3 = 7
C2R3: Median has to be greater than 5, hence condition 2 cannot be satisfied, hence conditions 1 and 3 have to be satisfied.
The first and third sacks have 1 and 9 coins respectively.
The second sack has more than 5 coins, such that the average is an integer. This is only possible when it has 8 coins.
∴ Average number of coins/sack = (1 + 8 + 9)/3 = 6
C2R2: If median is one, then first sack will also have 1 coin which would satisfy 2 of the given conditions, hence median cannot be 1.
Since all the values are less than or equal to 5, condition 3 cannot be satisfied.
Hence, the only condition that can be satisfied is the first condition that lowest number of coins is 1.
C1R2: **At least 2 conditions should be satisfied.
The median cannot be 1, hence the conditions to be satisfied are 1st and 3rd.
∴ Frist sack has 1 coin and third sack has 9 coins.
∴ Average number of coins/sack = (1 + 2 + 9)/3 = 4
C1R3: All sacks have more than 5 coins, hence condition 1 and 2 cannot be satisfied.
Hence, the only condition that can be satisfied is that the third sack has 9 coins.
Now, the two sacks have combined 8 + 9 = 17 coins.
The total should be a multiple of 3 (average is an integer), and the first sack has more than 5 coins. This is possible only when the third sack has 7 coins.
∴ Average number of coins/sack = (7 + 8 + 9)/3 = 8
C1R1: Since 2 conditions need to be satisfied and the average has to be an integer, this is possible when number of coins is 1, 1, 7 or 1, 5, 9
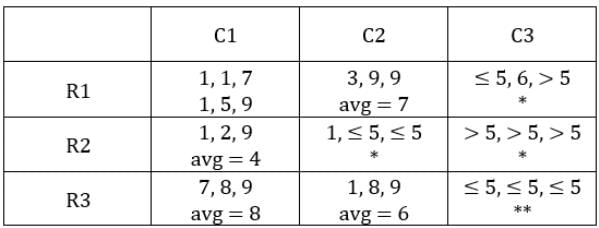
Case 1: C1R1 has 1, 5, 9 coins.
Total coins in C1 = 1 + 5 + 9 + 1 + 2 +9 + 7 + 8 + 9 = 51
Now C2 so far has = 3 + 9 + 9 + 1 + 1 + 8 + 9 = 40 coins
∴ C2 needs 51 – 40 = 11 more coins from two sacks in C2R2 block. This is not possible since these blocks have less than or equal to 5 coins each in them.
Hence, this case is rejected.
Case 2: C1R1 has 1, 1, 7 coins.
Total coins in C1 = 1 + 1 + 7 + 1 + 2 + 9 + 7 + 8 + 9 = 45
∴ Number of coins in the two sacks in C2R2 = 45 – 40 = 5 coins.
⇒ Number of coins in each column = 45.
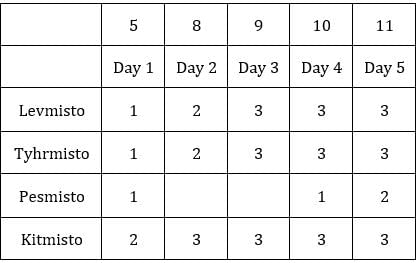
C2R2: Since first condition is satisfied, no other condition should be satisfied. Also, the sum of coins in second and third sack is 5. This is possible when the number of coins in them is 2 and 3 respectively.
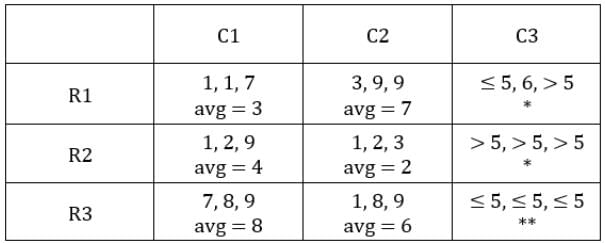
C3R3: All sacks have ≤ 5 coins hence condition 3 cannot be satisfied. Hence, the first two conditions should be satisfied.
⇒ The first and the second sacks have 1 coin each.
Since the average has to be an integer, the third sack can be 1 or 4 coins.
With 4 coins the average will become (1 + 1 + 4)/3 = 2 which cannot be the case since C2R1 already have average of 2 and all blocks have distinct averages.
∴ Third sack has 1 coin.
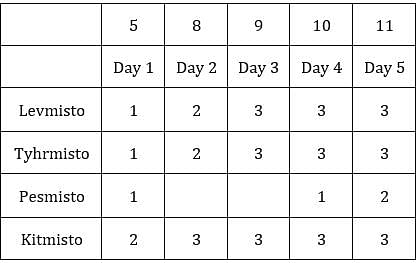
∴ Average number of coins/sack = (1 + 1 + 1)/3 = 1
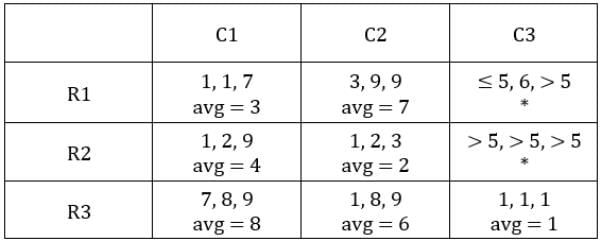
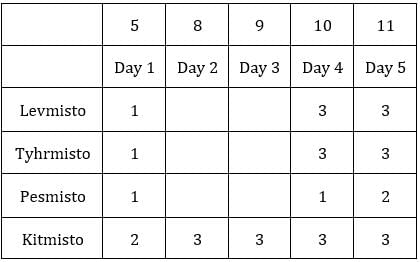
The averages so far have been, 1, 2, 3, 4, 6, 7, and 8. So C3R1 and C3R2 will have average 6 or 9 in any order.For average to be 9, all sacks must have exactly 9 coins. This is possible only for C3R2.
∴ Average for C3R2 is 9 and that for C3R1 is 5.
C3R1: will have a total of 5 × 3 = 15 coins.
Second sack has 6 coins, hence the other 2 sacks will have 15 – 6 = 9 coins.
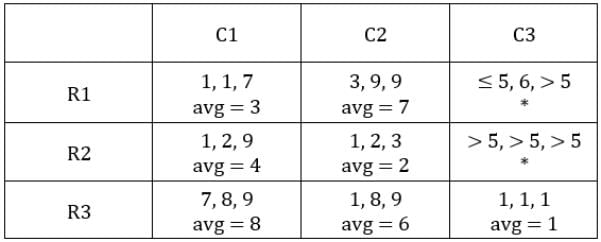
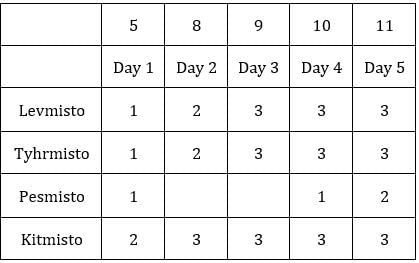
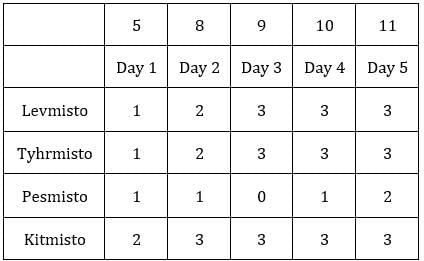
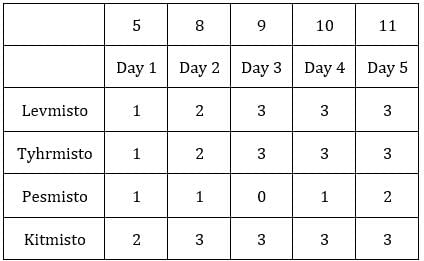
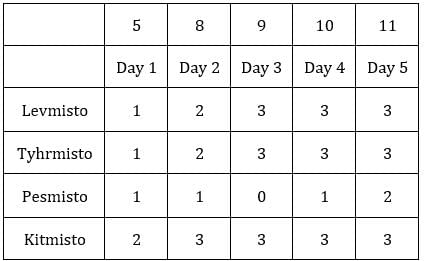
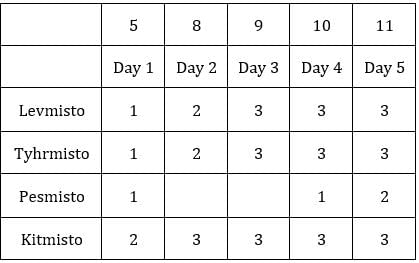
Since exactly one condition has to be satisfied, this is possible when first sack has 1 coin and third sack has 8 coins.Hence, we get the following final table.
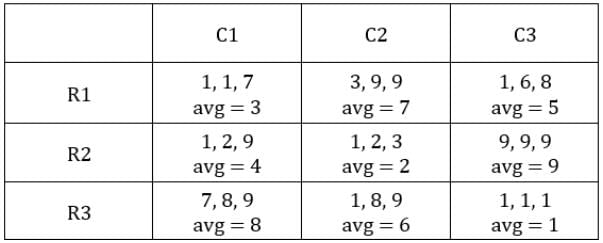
C1R2, C1R3, C2R1, C2R3 and C3R2 i.e., 5 blocks have at least one sack containing 9 coins.
Hence, option (c).